Решение (II способ).

1) Так как валовой выпуск продукции (ВВП) зависит от величины основных производственных фондов (ОПФ), то в качестве факторного признака (X) будет выступать стоимость ОПФ, а в качестве результативного (Y) – ВВП.

Уравнение линейной регрессии имеет вид:

,

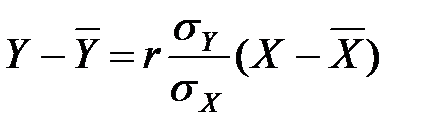где 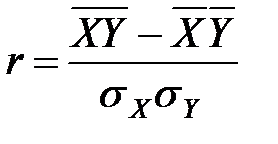– линейный коэффициент корреляции;

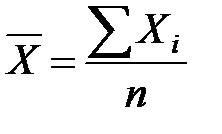– средняя стоимость ОПФ;

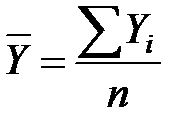– средняя величина ВВП;

;

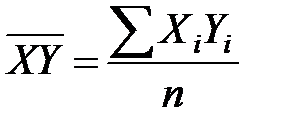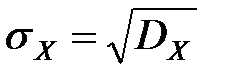– среднее квадратическое отклонение стоимости ОПФ;

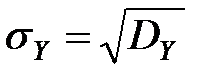– среднее квадратическое отклонение ВВП;

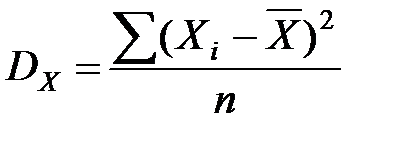– дисперсия стоимости ОПФ;

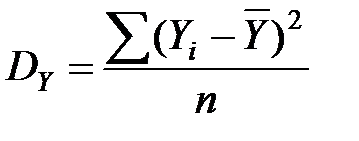– дисперсия ВВП;

Рассчитаем необходимые суммы в таблице:

	X	Y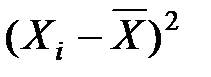
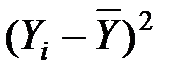
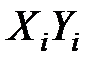
Итого

Тогда 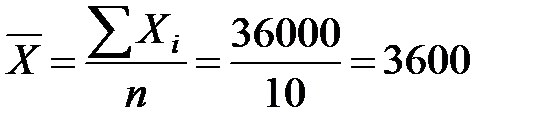(млн. руб.);

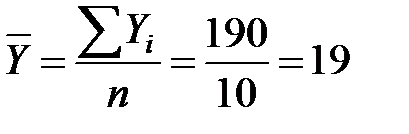(млн. руб.);

;

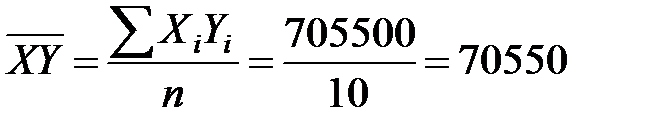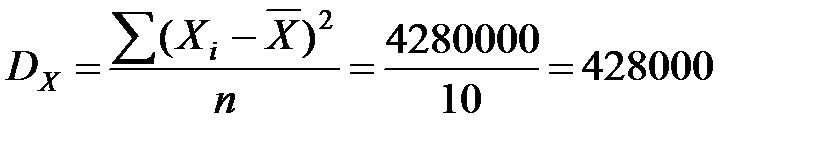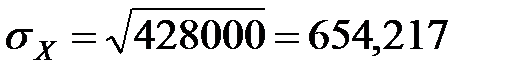; (млн. руб.);

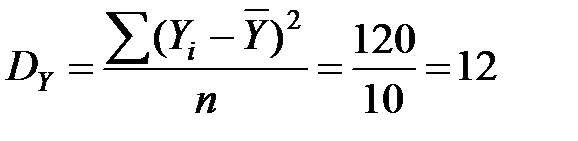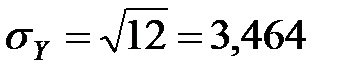; (млн. руб.);

;

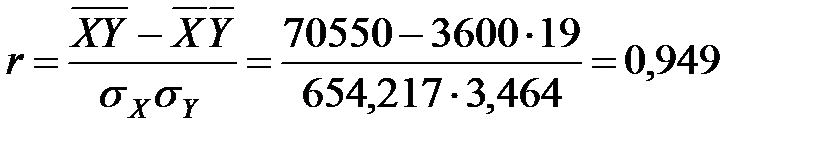Уравнение линейной регрессии имеет вид:

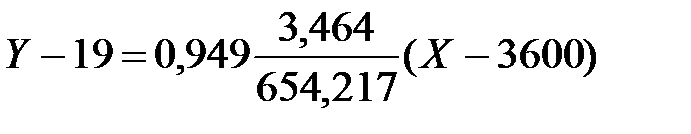или .

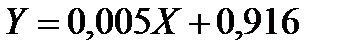2а) Линейный коэффициент корреляции 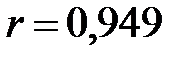свидетельствует о тесной связи между признаками, т.е. ВВП зависит от величины ОПФ.

2б) Коэффициент детерминации найдем по формуле:

,

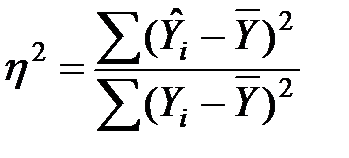где 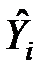– теоретические значения результативного признака, которые находим по уравнению регрессии.

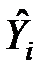
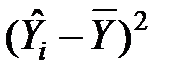
	16,488	6,309
	18,498	0,252
	19,000	0,000
	14,479	20,440
	15,986	9,084
	20,507	2,271
	21,512	6,309
	24,526	30,533
	23,521	20,440
	15,484	12,365
Итого		108,002

Тогда .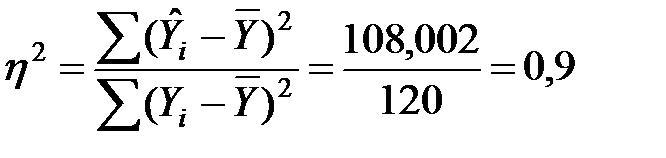

Коэффициент детерминации служит для оценки степени соответствия модели фактическим данным. Таким образом, 90 % вариации ВВП предприятий связана с вариацией стоимости ОПФ, т.е. модель объясняет наблюдаемые значения переменных на 90 %.

3) По построенной модели линейной регрессии можно осуществить прогноз ВВП, т.к. связь между указанными признаками достаточно тесная. На предприятии со стоимостью ОПФ 3700 млн. руб. можно ожидать ВВП: 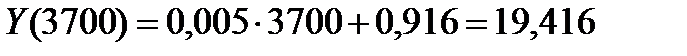млн. руб.

Если связь между признаками выражается какой-либо кривой линией, то нужно применить соответствующую формулу для расчета уравнения регрессии. Так, например, при связи, выраженной в форме гиперболы, уравнение регрессии имеет вид:

,

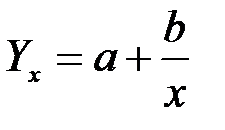Параметры уравнения 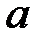и 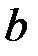находятся из решения системы уравнений: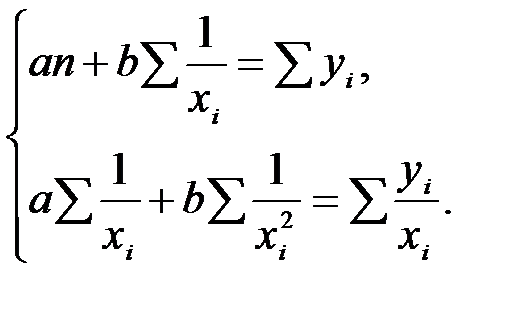

Если уравнение регрессии имеет форму параболы второго порядка, то его уравнение будет: .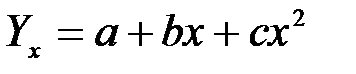

Параметры уравнения 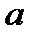, 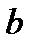и находятся из решения системы уравнений: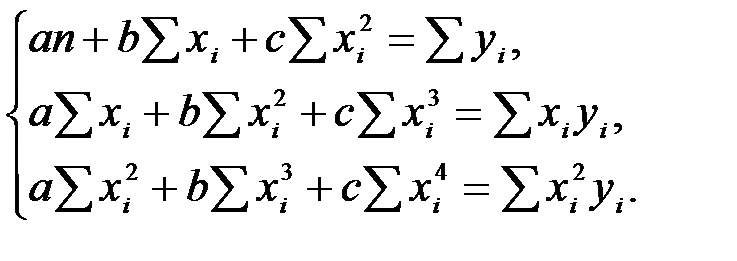

Показателем тесноты криволинейной корреляции является корреляционное отношение, которое вычисляется по выше приведенной формуле.