Линейное уравнение множественной регрессии
В парной корреляции исходят из постулата, что результативный признак зависит от одного факторного признака.
В действительности связь в экономических явлениях чаще является многофакторной. Уравнения, выражающие зависимость результативного признака от многих факторов, называются многофакторными (множественными) корреляционными уравнениями.
Линейное уравнение множественной регрессии в общем виде представляется формулой
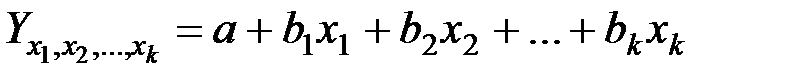 ,
,
где 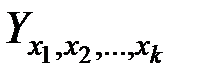 - значение результативного признака, соответствующее заданным факторным признакам
- значение результативного признака, соответствующее заданным факторным признакам 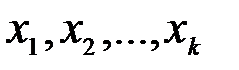 .
.
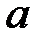 ,
, 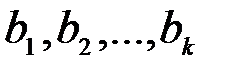 - параметры уравнения.
- параметры уравнения.
Параметр 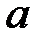 экономической интерпретации не имеет. Параметр
экономической интерпретации не имеет. Параметр 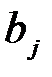 называется коэффициентом условно-чистой регрессии.
называется коэффициентом условно-чистой регрессии.
Термин «коэффициент условно-чистой регрессии» означает, что каждая из величин 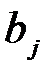 измеряет среднее по совокупности отклонение результативного признака от его средней величины при отклонении данного фактора
измеряет среднее по совокупности отклонение результативного признака от его средней величины при отклонении данного фактора 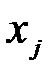 от своей средней величины на единицу его измерения и при условии, что все прочие факторы, входящие в уравнение регрессии, закреплены на средних значениях, не изменяются, не варьируют.
от своей средней величины на единицу его измерения и при условии, что все прочие факторы, входящие в уравнение регрессии, закреплены на средних значениях, не изменяются, не варьируют.
Таким образом, в отличие от коэффициента парной регрессии коэффициент условно-чистой регрессии измеряет влияние фактора, абстрагируясь от связи вариации этого фактора с вариацией остальных факторов. Если было бы возможным включить в уравнение регрессии все факторы, влияющие на вариацию результативного признака, то величины 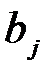 можно было бы считать мерами чистого влияния факторов. Но так как реально невозможно включить все факторы в уравнение, то коэффициенты
можно было бы считать мерами чистого влияния факторов. Но так как реально невозможно включить все факторы в уравнение, то коэффициенты 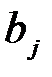 не свободны от примеси влияния факторов, не входящих в уравнение.
не свободны от примеси влияния факторов, не входящих в уравнение.
Параметры уравнения 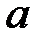 ,
, 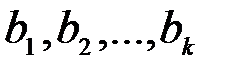 найдем из решения системы нормальных уравнений:
найдем из решения системы нормальных уравнений:
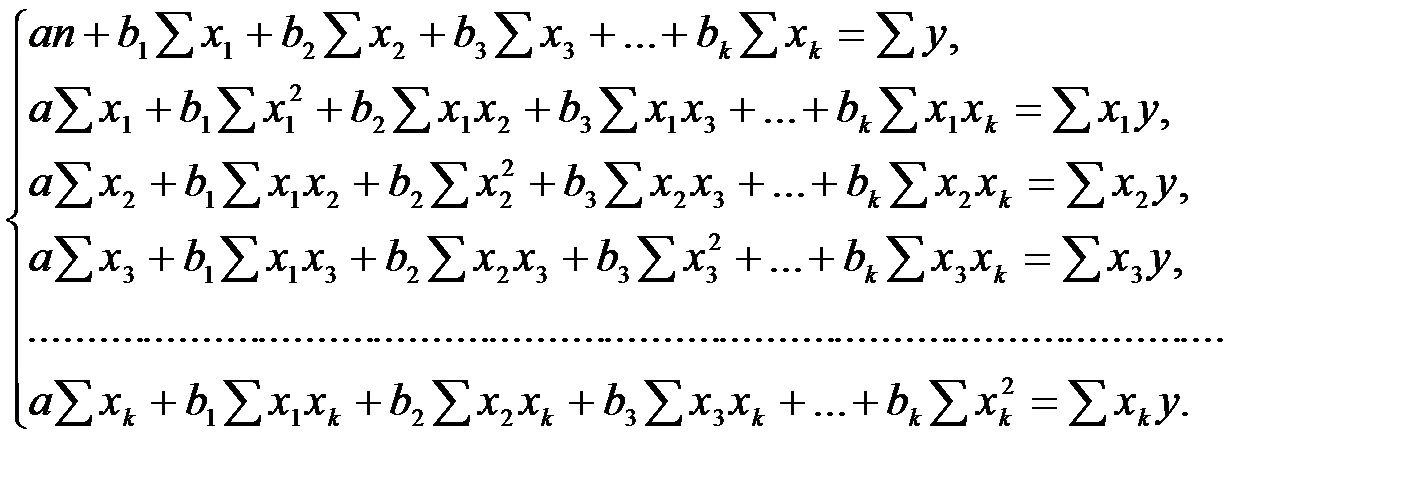
Уравнение множественной регрессии в нелинейной форме не применяют в связи с тем, что их решение в математическом плане становится сверхсложной задачей.
При построении уравнения множественной регрессии принципиальное значение приобретает отбор факторов, которые будут участвовать в данной модели.
Выбранная функция должна отразить основные закономерности, но в то же время иметь по возможности простой вид.
Отбор факторов для модели может быть выполнен в следующей последовательности.
На первой стадии производится априорный анализ явления и устанавливаются все возможные факторы.
На второй стадии осуществляется сравнительная оценка и отсев части факторов с помощью парных коэффициентов корреляции.
Если абсолютная величина парного коэффициента корреляции 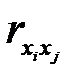 =0,8 и более то факторы
=0,8 и более то факторы 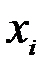 и
и 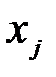 считаются коллинеарными (дублирующими друг друга) и один из них отбрасывается.
считаются коллинеарными (дублирующими друг друга) и один из них отбрасывается.
На третьей стадии выполняется многошаговый процесс вычислений с последовательным отсевом наименее значимого фактора 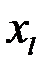 , у которого парный коэффициент корреляции
, у которого парный коэффициент корреляции 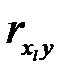 оказался наименьшим.
оказался наименьшим.
Для каждой модели, включающей в себя число факторов, последовательно уменьшенное на один из них, рассчитывается совокупный коэффициент корреляции или корреляционное отношение, которые равны между собой. Модель с наибольшим совокупным коэффициентом (или корреляционным отношением) считается наиболее оптимальной.
Рассмотрим множественное уравнение регрессии с двумя признаками-факторами:
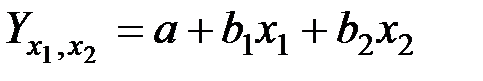 .
.
Параметры уравнения найдем из решения системы нормальных уравнений:
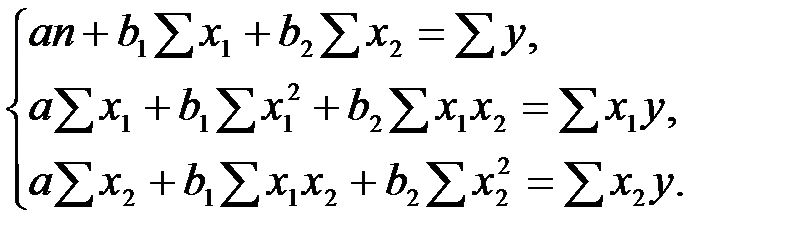
Совокупный коэффициент корреляции находится по формуле:
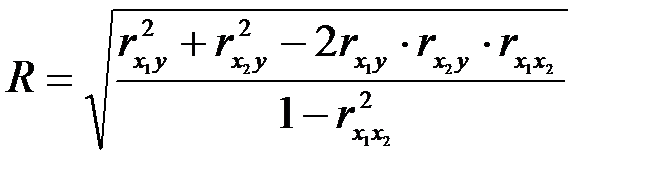 .
.
Корреляционного отношения вычисляется по формуле:
 ,
,
где 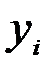 - индивидуальные значения результативного признака,
- индивидуальные значения результативного признака,
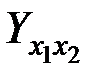 - теоретические значения результативного признака, которые находятся по уравнению множественной регрессии,
- теоретические значения результативного признака, которые находятся по уравнению множественной регрессии,
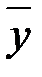 - среднее значение результативного признака.
- среднее значение результативного признака.
При этом совокупный коэффициент корреляции равен корреляционному отношению.
Дата добавления: 2015-02-13; просмотров: 1645;
