Изображение экспериментальных результатов на графиках

Результаты экспериментов обычно представляют не только в виде таблиц, но и в графической форме. Для графиков следует использовать специальную бумагу (миллиметровую, логарифмическую или полулогарифмическую). При их отсутствии иногда приходится (хотя это крайне нежелательно!) пользоваться бумагой «в клеточку» или белой бумагой, на которой карандашом нанесена сетка. Не следует выбирать слишком малый или слишком большой лист бумаги. Удобна бумага размером в обычный тетрадный лист (или в развернутый лист). Полезно пользоваться листами миллиметровки из блокнотов (или планшетов) для диаграмм.

При построении графиков следует разумно выбирать масштабы, чтобы измеренные точки располагались на всей площади листа. Масштаб должен быть удобным. Клеточка графика (или миллиметр миллиметровой бумаги) может соответствовать 0,1; 0,2; 0,5; 1; 2; 5; 10 и т. д. единицам измеряемой величины, но не 2,5; 3; 4; 7 и т. д. При неудобном масштабе нанесение экспериментальных точек на график и использование графика требуют неоправданно большого времени и нередко сопровождаются досадными ошибками.

Графическое представление результатов позволяет быстро понять характерные черты наблюдаемой зависимости и обнаружить ошибочные результаты. При рассмотрении графика можно увидеть, что какая либо точка выпадает из закономерности. Это может означать, что при ее измерении была допущена ошибка. Если это не так, то в районе этой точки искомая зависимость имеет резко выраженную особенность. Именно такие особенности и представляют наибольший интерес для экспериментатора. Поэтому нужно внимательно промерить область, расположенную вблизи выпавшей точки, и постараться детально изучить форму кривой в районе найденной особенности.

Точки, наносимые на графики, должны изображаться четко и ясно. Их следует отмечать карандашом, так как иначе ошибочно нанесенную точку нельзя удалить с графика, не испортив его. Никаких линий и отметок, поясняющих построение точек, на график наносить нельзя, так как они загромождают рисунок и мешают анализировать результаты.

Точки, полученные в разных условиях (при нагревании и при охлаждении, при увеличении и при уменьшении нагрузки, в разные дни и т. д.), полезно наносить разными цветами или разными значками. Это помогает увидеть новые явления.

Способ изображения на графике экспериментальных результатов зависит от того, известна ли их случайная погрешность. Если случайная погрешность неизвестна (что чаще всего и бывает), то результаты изображаются точками, а если известна, то лучше изображать их не точками, а крестами.

Полуразмер креста по горизонтали должен быть равен стандартной погрешности по оси абсцисс, а его вертикальный полуразмер - погрешности по оси ординат.

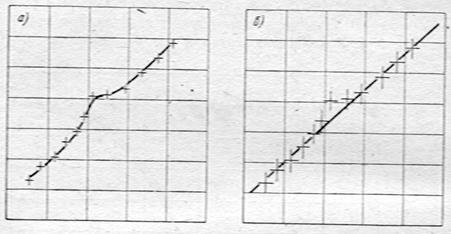
В том случае, если одна из ошибок - из-за своей малости - не может быть изображена графически, результаты изображаются черточками, вытянутыми на величину ±s в том направлении, где погрешность не мала. Важность такого способа изображения результатов ясна из рисунков, на которых изображены одни и те же экспериментальные точки при разных погрешностях измерений.

График (а) несомненно, указывает на нерегулярный ход изучаемой зависимости. Эта зависимость изображена на рисунке кривой линией.

Те же данные при больших ошибках опыта (б) с успехом описываются прямой линией, так как только одно измерение отступает от этой кривой больше, чем на стандартную ошибку (и меньше, чем на две такие ошибки).

То обстоятельство, что при ошибках на (а) данные требуют проведения кривой, а на (б) этого не требуют, проясняется лишь при изображении экспериментальных результатов в виде креста погрешностей.

Из сказанного отнюдь не следует, что, изображая результаты опытов не крестами погрешностей, а простыми точками, мы всегда совершаем ошибку. Если величины погрешностей уже ясны при построении графика, следует, конечно, их изображать. Чаще всего, однако, эти погрешности к моменту построения графика неизвестны, и их разумно определять из разброса точек на графике. В этих случаях экспериментальные данные естественно изображать простыми точками.

Заметим также, что кривые на графиках не всегда проводятся через экспериментальные точки. Нередко кривые изображают зависимость, полученную не из эксперимента, а из теоретических соображений (или из других опытов). При построении таких кривых возникает необходимость предварительно нанести на график ряд расчетных точек. Эти точки должны наноситься еле заметным образом, чтобы их нельзя было спутать с четкими точками (или крестами), изображающими экспериментальные данные. Лучше всего, чтобы расчетные точки вообще не были заметны.

Оси графика должны иметь ясные, четкие обозначения. Рядом с делениями, на удобных расстояниях, должны быть нанесены цифры, позволяющие установить значения, соответствующие делениям шкалы. Цифры принято располагать по краям сетки. На графиках должно быть указано, какая физическая величина и в каком масштабе на ней отложена.

Проведение кривых через экспериментальные точки: Через экспериментальные точки всегда следует проводить самую простую кривую, совместимую с этими точками, т.е. кривую, от которой экспериментальные данные отступают, как правило (в 2/3 случаев), не более чем на стандартную ошибку. Примеры таких кривых и изображены на рисунке. Не следует придавать кривым никаких изгибов, если экспериментальным данным, в пределах ошибок, можно удовлетворить и без этого.

При проведении кривой нужно следить за тем, чтобы на каждом достаточно большом ее участке экспериментальные точки располагались как выше, так и ниже кривой. Так, на рис. а левая часть кривой изображена верно, а правая – неверно, т.к. ни одна из точек графика не лежит выше этой части кривой.

Математическое правило проведения кривых заключается в следующем. После того как тип кривой (прямая, окружность, парабола, и т.д.) из тех или иных соображений (чаще всего теоретических) выбран, параметры кривой должны быть подобраны так, чтобы сумма квадратов отклонения от нее всех экспериментальных точек была наименьшей (правило «наименьших квадратов»). Пользоваться этим правилом при графическом изображении экспериментальных зависимостей затруднительно, но при некотором опыте графические изображения данных измерений оказываются практически оптимальными.

При графической обработке результатов следует помнить, что на глаз точно провести через экспериментальные точки можно только прямую линию. Поэтому при построении графика следует стремиться к тому, чтобы ожидаемая зависимость имела вид прямой линии.

Так, исследуя закон падения тел, мы вправе ожидать, что результаты будут описываться законом S = gt²/2. Если откладывать по осям графика S и t, то точки лягут на параболу, которую провести на глаз почти невозможно. Но если откладывать по осям S и t², или S и gt²/2, то график приобретет вид прямой линии. Одно из этих представлений и должно быть выбрано для построения графика.

Производя измерения, всегда следует заботиться о том, чтобы точки на графике, который потом будет построен, располагались достаточно равномерно. В нашем примере, решив, например, строить график в переменных S и t², следует выбирать время измерений так, чтобы точки лежали на равных расстояниях в шкале t², а не t. Выбор равных интервалов времени (0,5; 1; 1,5; 2 с. и т.д.) приведет к тому, что в правой части графика точки будут лежать редко, а в левой части - слишком близко друг к другу.

К логарифмическому масштабу без особой необходимости прибегать не следует.

Одна из наиболее часто встречающихся погрешностей опыта - смещение нуля отсчета - приводит к сильному искажению прямолинейного характера кривой. В самом деле, пусть из-за смещения линейки вместо длин S на опыте будет найдено S₁ = S + а где, а - постоянная для всех точек ошибка. Формула, связывающая измеренную длину и время, в этом случае будет иметь вид S_t = (gt²/2) + а. В координатах S и t² эта зависимость изображается прямой линией, которая на этот раз не проходит через начало координат. По смещению прямой мы легко заметим ошибку и даже найдем ее величину. А в переменных lgS и lgt кривая теряет прямолинейный вид, и будет нелегко сообразить, где же вкралась ошибка.

Бывают, однако, случаи, когда логарифмический масштаб необходим. Это происходит, например, если исследуемая величина очень сильно изменяется, причем одновременно интересны очень малые и очень большие ее значения. Логарифмический масштаб позволяет все точки уместить на одном чертеже и исследовать совместно. Логарифмический масштаб выбирают и в том случае, если имеются основания ожидать, что искомая зависимость является степенной, но показатель степени неизвестен.