Погрешности измерений. Говоря о погрешностях измерений, следует, прежде всего, упомянуть о грубых погрешностях (промахах), возникающих вследствие недосмотра оператора или

Говоря о погрешностях измерений, следует, прежде всего, упомянуть о грубых погрешностях (промахах), возникающих вследствие недосмотра оператора или неисправности аппаратуры. Такие ошибки происходят, если, например, экспериментатор неправильно прочтет номер деления на шкале, если в электрической цепи произойдет замыкание и вследствие других подобных причин. Грубых ошибок следует избегать. Если установлено, что они произошли, соответствующие измерения нужно отбрасывать.

Не связанные с грубыми ошибками погрешности измерений бывают - случайные и систематические.

Погрешности измерений выявляют путем сравнения результатов, полученных при нескольких опытах, поставленных в одинаковых условиях. Два-три измерения следует производить всегда. Если результаты совпали, то на этом следует остановиться. Если же они расходятся, нужно попытаться понять причину расхождения. Часто она связана с тем, что прибор неисправен, ненадежно закреплен или плохо смазан, что электрические контакты не пропаяны или недостаточно зажаты. В этом случае, прежде всего, нужно попытаться исправить аппаратуру. Если устранить причину не удается, нужно произвести несколько измерений и записать все полученные результаты. Ниже будет рассказано о том, как следует поступать с полученными числами.

Многократно повторяя одни и те же измерения, можно заметить, что довольно часто их результаты не в точности равны друг другу, а «пляшут» вокруг некоторого среднего. Погрешности, меняющие величину и знак от опыта и опыту, называют случайными.

Случайные погрешности могут быть связаны с трением, из-за которого приборная стрелка, вместо того чтобы останавливаться в правильном положении, «застревает» вблизи него; с люфтами в механических приспособлениях; с тряской, которую в городских условиях трудно исключить; с несовершенством объекта измерений (например, при измерении диаметра проволоки, которая, из-за случайных причин, возникающих при изготовлении, имеет не вполне круглое сечение) или с физическими особенностями самой измеряемой величины.

Систематические погрешности сохраняют свою величину (и знак!) во время эксперимента.

Они могут быть связаны с ошибками приборов (неправильная шкала, неравномерно растягивающаяся пружина, неравномерный шаг микрометрического винта, не равные плечи весов) и с самой постановкой опыта (определение скорости поезда по проходимому им расстоянию на участке, где движение происходит с небольшим ускорением, которое ускользнуло от внимания оператора, влияние трения и т. д.).

В результате систематических погрешностей, разбросанные из-за случайных ошибок результаты опыта колеблются не вокруг истинного, а вокруг некоторого смещенного значения.

Рис. 1 поясняет различие между случайными и систематическими погрешностями.

В ситуации, изображенной на рис. 1, а, систематическая погрешность пренебрежимо мала. Измеренные значения отличаются от истинного вследствие случайных ошибок опыта. На рис. 1, б изображены результаты опыта при наличии как случайных, так и систематических погрешностей.

Систематические погрешности опыта могут быть изучены и скомпенсированы, путем внесения поправок в результаты измерений.

Неравноплечность весов можно учесть, меняя местами грузы на чашках весов.

Неточность шкал электроизмерительных приборов можно установить, сравнивая их показания с показаниями более точных приборов, и т. д.

Различие между случайными и систематическими погрешностями не является абсолютным. Оно связано с постановкой измерительного эксперимента.

Например, производя измерения тока несколькими разными амперметрами систематическую ошибку, связанную с неточностью шкалы, мы превращаем в случайную, величина (и знак!) которой зависит от того, какой поставлен амперметр в данном опыте и т.д.

Однако, во всяком данном опыте - при заданной его постановке - различие между систематическими и случайными погрешностями всегда можно и нужно устанавливать с полной определенностью.

Случайные погрешности изучаются в теории вероятностей и в математической статистике.

Рассмотрим для примера данные, полученные при измерениях массы тела на весах, у которых имеется область застоя из-за трения призмы на подушке. Пусть масса тела близка к 48 мг, результат измерений удается отсчитать по шкале с точностью до 0,1 мг. Имеем в миллиграммах: 48,0; 47,9; 47,5; 48,2; 48,4; 47,8; 48,6; 48,3; 47,8; 48,1; 48,2. Вместо одного нужного нам результата мы получили одиннадцать.

Что делать с полученными цифрами? Как найти действительное значение массы тела и как оценить погрешность полученного результата?

Этот вопрос подробно изучается в математической статистике. Рассмотрим соответствующие правила без вывода.

В качестве наилучшего значения для измеренной величины обычно принимают среднее арифметическое из всех полученных результатов:

(26)

в нашем случае получим

Этому результату следует приписать погрешность, определяемую формулой

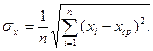(27)

В нашем случае

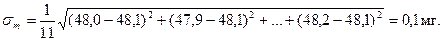
Результат опыта записывается в виде

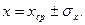(28)

В нашем случае m = (48,1 ± 0,1) мг.

Рассмотрим формулы (26) и (27). Прежде всего, попытаемся понять, как зависит результат расчета от числа измерений.

Формула (26) показывает, что х_ср слабо зависит от числа измерений. Все слагаемые, входящие в числитель, приблизительно равны друг другу. Их сумма пропорциональна числу слагаемых. После деления на знаменатель получается величина, мало зависящая от числа измерений, Так, конечно, и должно быть. Среднее измеренное значение - при правильной методике опыта - всегда лежит вблизи истинного значения и в разных независимых сериях измерений испытывает вокруг него небольшие случайные колебания.

Погрешность опыта, определяемая формулой (27), с увеличением числа измерений n уменьшается как Ön:

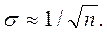(29)

(Число членов суммы в (27) растет как n, числитель (27) поэтому увеличивается как Ön, а все выражение уменьшается как Ön.)

Этот результат является очень важным.

По мере увеличения числа опытов ошибки в сторону преувеличения и преуменьшения результата все лучше компенсируют друг друга, и среднее значение приближается к истинному.

В нашем примере одиночные отсчёты отличаются от среднего на несколько десятых, а погрешность результата, полученного при усреднении всех измерений, составляет всего одну десятую.

Корень из n определяет среднеквадратичную погрешность одного измерения. При обсуждении смысла величины s следует помнить, что истинную величину погрешности невозможно узнать до тех пор, пока из каких-либо других опытов (или соображений) не удастся определить искомую величину с существенно лучшей точностью.

Как уже отмечалось, погрешность результата не столько определяют, сколько оценивают. Оценка (27) подобрана так, что при проведении многочисленных серий измерений погрешность в 2/3 случаев оказывается меньше s_х, а в 1/3 случаев больше, чем s_х .

Иначе говоря, если провести не одну серию из 11 взвешиваний, а десять таких серий, то можно ожидать, что в шести или семи из них усредненный результат будет отличаться от истинной массы тела меньше чем на 0,1 мг, а в остальных случаях больше чем на 0,1 мг.

Погрешность, определенную с достоверностью 2/3, обычно называют стандартной (или среднеквадратичной) погрешностью измерений, а её квадрат - дисперсией. Можно показать, что, как правило, погрешность опыта только в 5% случаев превосходит ±2s и почти всегда оказывается меньше ±3s.

На первый взгляд из сказанного можно сделать вывод, что, беспредельно увеличивая число измерений, можно даже с самой примитивной аппаратурой получить очень хорошие результаты.

Это, конечно, не так.

С увеличением числа измерений уменьшается только случайная погрешность опытов. Методические погрешности и погрешности, связанные с несовершенством приборов (например, с неправильностью их шкалы), при увеличении числа опытов ведут себя скорее наоборот и в лучшем случае не меняются.

В приведенном выше примере результат взвешивания округлялся до десятых долей миллиграмма. Это делалось потому, что сотых долей отсчитать было нельзя. Ошибка отсчета составляла при этом около 0,1 мг. Поэтому погрешность результата, ни при каком числе опытов не может быть сделана меньше. Число опытов в нашем случае было выбрано разумно.

Из приведенных в таблице цифр ясно, что при однократном измерении можно ошибиться на несколько десятых. Среди цифр, встречаются результаты, отличающиеся на 0,3 и даже на 0,5 от среднего. После усреднения по 11 измерениям погрешность существенно уменьшилась.

Но если окажется нужным узнать массу тела с лучшей точностью, то недостаточно просто увеличить число измерений. Придется взять более точные весы, позволяющие производить измерения не до десятых, а, скажем, до сотых долей миллиграмма.

Необходимо заметить, что формула (27) позволяет хорошо оценивать величину стандартной погрешности только в тех случаях, когда число опытов оказывается не меньше 4 ¸ 5.

При меньшем числе опытов лучше применять другие, более сложные оценки.

Однако надежность всех этих оценок при малом числе измерений оказывается невысокой.

Систематические погрешности. Оценку систематических погрешностей экспериментатор производит, анализируя особенности методики, паспортную точность приборов и производя контрольные опыты.

Отметим различие в правилах определения погрешностей и в определении класса точности.

Погрешности принято характеризовать среднеквадратичными ошибками. При многочисленных измерениях реальная ошибка опытов только в 2/3 случаев меньше среднеквадратичной, а в 1/3 случаев превосходит её.

Класс точности определяет максимально возможное значение погрешности. Приборы, которые могут давать, хотя бы иногда, бо^¢льшие погрешности, должны быть отнесены к другому классу.

Такое различие в определениях неудобно. В научных публикациях принято приводить именно среднеквадратичную ошибку, а вовсе не максимальную. Строгих формул для перевода одних погрешностей в другие не существует, поэтому можно пользоваться следующим простым правилом: чтобы оценить среднеквадратичную погрешность измерений приборами, следует погрешность, определяемую классом точности прибора, разделить на два.

Как уже отмечалось, класс приборов определяет максимальную погрешность, величина которой не меняется при переходе от начала к концу шкалы. Относительная ошибка при этом резко меняется, поэтому приборы обеспечивают хорошую точность при отклонении на всю шкалу и не дают её при измерениях в начале шкалы. Отсюда следует рекомендация: выбирать прибор (или шкалу многошкального прибора) так, чтобы стрелка прибора при измерениях заходила за середину шкалы.

Говоря о систематических погрешностях измерений в механике, следует сказать несколько слов об ошибке отсчета «на глаз». Большинство приборов не имеет нониусных шкал. При этом доли деления отсчитываются на глаз. Эта ошибка составляет 1 - 2 десятых доли деления. При отсчётах следует следить за тем, чтобы луч зрения был перпендикулярен шкале. Для облегчения установки глаза на многих приборах устанавливается зеркало (зеркальные приборы). Глаз оператора установлен правильно, если стрелка прибора закрывает свое изображение в зеркале. При работе с электроизмерительными приборами отсчет должен включать число целых делений и число десятых долей деления, если отсчет может быть произведен с этой точностью (если стрелка или зайчик не ходят и не дрожат, что может сделать аккуратный отсчет невозможным).

Поясним указанное правило. Шалы электроизмерительных приборов обычно изготовляют так, что одно деление шкалы приблизительно равно максимальной погрешности прибора. Зачем же в этом случае отсчитывать десятые доли деления? Дело в том, что при измерениях, при расчетах и при записи результатов, кроме надежно известных значащих цифр, всегда указывается одна лишняя. Такая процедура, среди прочих, имеет и то преимущество, что позволяет вовремя замечать, мелкие нерегулярности и исследуемых зависимостей. Если, например, стрелка прибора при измерениях отклонилась на полделения назад, этот результат является надежным и в том случае, когда погрешность прибора равна целому делению.

Несколько слов о точности линеек. Металлические линейки очень точны: миллиметровые деления наносятся с погрешностью не более ± 0,05 мм, а сантиметровые - не хуже, чем с точностью 0,1 мм. Погрешность измерений, производимых с помощью таких линеек, практически равна погрешности отсчета на глаз. Деревянными или пластиковыми линейками лучше не пользоваться: их погрешности неизвестны и могут оказаться неожиданно большими. Исправный микрометр обеспечивает точность 0,01 мм, а погрешность измерений штангенциркулем определяется точностью, с которой может быть сделан отсчет, т. е. точностью нониуса (у штангенциркулей цена делений нониуса составляет обычно 0,1 или 0,05 мм).