Устойчивость процессов в нелинейных системах

Основные понятия и определения

Раздел, посвященный анализу устойчивости систем автоматического управления, является традиционным при изложении курса ТАУ. Объясняется это тем, что системы управления с обратными связями (кибернетические системы) склонны к неустойчивости. Устойчивостью любого явления в природе называют его способность достаточно длительно сохранять те формы своего существования, при утрате которых явление перестает существовать. Применительно к САУ этими явлениями являются протекающие в них процессы.

Основные определения и методы анализа устойчивости были даны в работах крупнейшего российского математика Ляпунова А.М.

Рассмотрим простейший случай нелинейной системы первого порядка рис. 2.2, которая описывается нелинейным дифференциальным уравнением

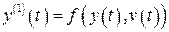, (2.68)

где 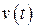− входное воздействие, 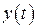− исследуемая координата.

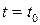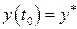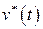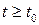Пусть при задано начальное значение искомого решения и задано определенное входное воздействие при . В этом случае уравнение (2.68) имеет определенное решение 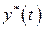, которое будем называть невозмущенным процессом (решением, движением). Любое другое решение, обусловленное другими начальными условиями 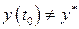, но при том же воздействии 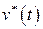, будем называть возмущенным и обозначать 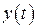. Задача ставится следующим образом: как ведет себя возмущенное движение 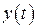относительно невозмущенного 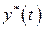с течением времени, т.е. при 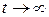, или как ведет себя отклонение 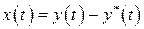при 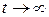. Решение этой задачи и составляет предмет математической теории устойчивости.

Анализ поведения решений исходного уравнения можно заменить анализом тривиального решения 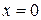уравнения

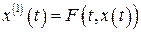, (2.69)

полученного из (2.68) заменой .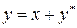

Уравнение (2.68) называется уравнением возмущенного движения в отклонениях. Это уравнение всегда имеет решение .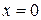

Рассмотрим общий случай нелинейной системы произвольного порядка, для которой уравнения возмущенного движения в отклонениях имеют вид:

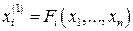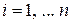, , (2.70)

где при 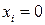функции .

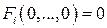Дадим ряд понятий и определений устойчивости, следуя работам Ляпунова.

Невозмущенное решение 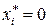(положение равновесия) называется устойчивым, если при заданном 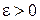, сколь бы оно мало ни было, существует такое 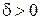, в общем случае зависящее от 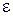, что при начальных отклонениях 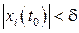, 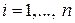будет выполняться условие 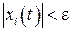, 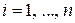при .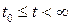

Невозмущенное решение 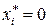называется неустойчивым, если хотя бы для одного 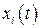условие 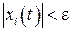не выполняется.

Если решение 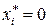устойчиво и дополнительно при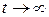 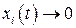, , 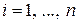то невозмущенное решение 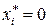будем называть асимптотически устойчивым.

Если положение равновесия асимптотически устойчиво при любых начальных отклонениях 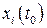, т.е. 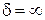, то говорят об устойчивости в целом. Если известна величина 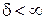, то говорят об устойчивости в большом или об устойчивости в области. Если известно, что величина 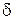существует и может быть сколь угодно малой, то говорят об устойчивости в малом.

Наконец, если положение равновесия асимптотически устойчиво в целом при любых нелинейных функциях 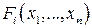из заданного класса, то говорят об абсолютной устойчивости нелинейной системы (2.70).

Отметим, что в случае линейной системы положение равновесия устойчиво (асимптотически устойчиво) при любых отклонениях, т.е. устойчиво в целом. Кроме этого следует помнить, что устойчивость линейных систем не зависит от характера внешних воздействий, т.е. в этом плане устойчивость (неустойчивость) линейных систем является ее внутренним свойством.