Частотный метод определения симметричных колебаний
Передаточная функция разомкнутой нелинейной САУ рис. 2.2 будет 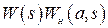 , где
, где 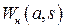 имеет вид (2.48), а АФЧХ разомкнутой системы соответственно будет
имеет вид (2.48), а АФЧХ разомкнутой системы соответственно будет 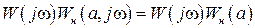 , где
, где 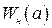 имеет вид (2.49), т.е.
имеет вид (2.49), т.е.
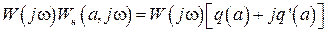 .
.
Наличие в характеристическом уравнении пары чисто мнимых корней 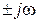 , соответствующих периодическому режиму
, соответствующих периодическому режиму 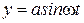 , в соответствии с критерием устойчивости Найквиста будет в том случае, если АФЧХ разомкнутой системы в комплексной плоскости пройдет через точку с координатами
, в соответствии с критерием устойчивости Найквиста будет в том случае, если АФЧХ разомкнутой системы в комплексной плоскости пройдет через точку с координатами 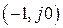 , т.е. должно выполняться условие
, т.е. должно выполняться условие
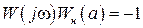 ,
,
или
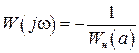 , (2.64)
, (2.64)
где 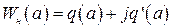 .
.
Решение уравнения (2.64), если оно существует, определяет амплитуду 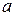 и частоту
и частоту 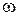 искомого периодического режима. Это уравнение можно решить аналитически, выделив действительные и мнимые части и приравняв их друг к другу, либо графическими. В последнем случае на комплексной плоскости наносится АФЧХ линейной части
искомого периодического режима. Это уравнение можно решить аналитически, выделив действительные и мнимые части и приравняв их друг к другу, либо графическими. В последнем случае на комплексной плоскости наносится АФЧХ линейной части 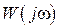 и обратная амплитудно-фазовая характеристика нелинейности с обратным знаком
и обратная амплитудно-фазовая характеристика нелинейности с обратным знаком 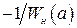 . В точке их перечисления по кривой
. В точке их перечисления по кривой 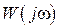 находится частота
находится частота 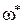 , а по кривой
, а по кривой 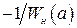 амплитуда
амплитуда 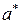 искомого периодического режима, как это изображено на рис. 2.17.
искомого периодического режима, как это изображено на рис. 2.17.
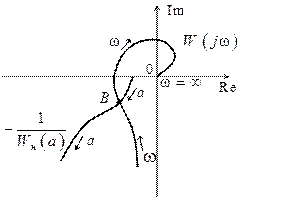

Рис. 2.17
Для определения периодического режима можно воспользоваться логарифмическими характеристиками. Из (2.64) можно получить
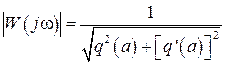 ,
,
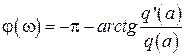 .
.
Вводя логарифмическую характеристику 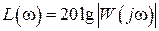 , можно записать
, можно записать
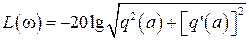 , (2.65)
, (2.65)
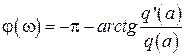 . (2.66)
. (2.66)
Выражения (2.65) и (2.66) называют балансом амплитуд и фаз.
В соответствии с (2.65), (2.66) строятся четыре графика: 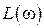 ,
, 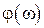 , соответствующие линейной части, и
, соответствующие линейной части, и 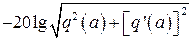 ,
, 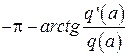 , соответствующие нелинейному элементу. Частота
, соответствующие нелинейному элементу. Частота 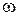 откладывается в логарифмическом масштабе, амплитуда
откладывается в логарифмическом масштабе, амплитуда 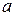 в обычном. Далее находятся такие
в обычном. Далее находятся такие 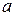 и
и 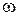 , при которых (2.65), (2.66) выполняются. Наиболее просто
, при которых (2.65), (2.66) выполняются. Наиболее просто 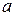 и
и 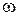 определяются для однозначных нечетно-симметричных нелинейностей, для которых
определяются для однозначных нечетно-симметричных нелинейностей, для которых 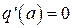 .
.
Для определения устойчивости периодического режима, если он существует, можно воспользоваться следующим приближенным правилом [3]: если при движении по кривой 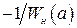 в сторону возрастания величины
в сторону возрастания величины 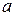 пересечение кривой
пересечение кривой 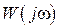 происходит изнутри наружу, то найденный режим устойчив, если наоборот, то неустойчив. На рис. 2.17 показан случай устойчивого периодического режима.
происходит изнутри наружу, то найденный режим устойчив, если наоборот, то неустойчив. На рис. 2.17 показан случай устойчивого периодического режима.
Отметим следующую особенность возникновения периодических режимов, исходя из изложенного метода гармонического баланса. Для нелинейностей, у которых 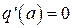 , характеристика
, характеристика 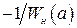 совпадает с отрезком, лежащим на отрицательной полуоси действительной оси. Ввиду этого, если
совпадает с отрезком, лежащим на отрицательной полуоси действительной оси. Ввиду этого, если 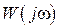 при изменении
при изменении 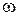 от 0 до
от 0 до 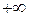 полностью находится в третьем и четвертом квадрантах комплексной плоскости, т.е. АФЧХ не пересекает отрицательную полуось, то периодические режимы в такой системе невозможны. Например, если передаточная функция линейной части имеет вид
полностью находится в третьем и четвертом квадрантах комплексной плоскости, т.е. АФЧХ не пересекает отрицательную полуось, то периодические режимы в такой системе невозможны. Например, если передаточная функция линейной части имеет вид
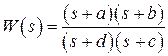 ,
,
то при 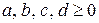 в случае
в случае 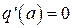 периодических режимов в системе не будет.
периодических режимов в системе не будет.
Пример 2.5. Рассмотрим систему с нелинейностью в виде идеального реле с зоной нечувствительности, для которой
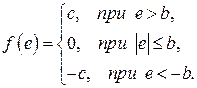
а передаточная функция нелинейной части имеет вид
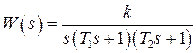 .
.
Для данного вида нелинейности 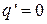 , а коэффициент
, а коэффициент 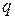 определяется выражением
определяется выражением
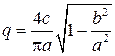 ,
, 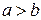 .
.
Зависимость 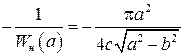 .
.
На рис. 2.18 изображены графики 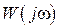 и
и 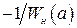 . Последняя характеристика имеет две ветви, совпадающие с отрицательным отрезком действительной оси. При изменении
. Последняя характеристика имеет две ветви, совпадающие с отрицательным отрезком действительной оси. При изменении 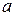 от
от 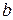 до
до 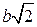 происходит движение изображений точки слева направо по верхней ветви кривой
происходит движение изображений точки слева направо по верхней ветви кривой 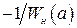 , а при
, а при 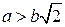 – вдоль нижней ветви кривой. При
– вдоль нижней ветви кривой. При 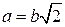 выполняется соотношение
выполняется соотношение 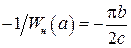 .
.
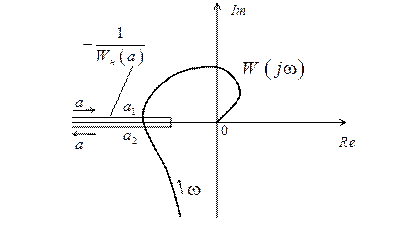
Рис. 2.18
Выражения АЧХ и ФЧХ линейной части системы имеют вид:
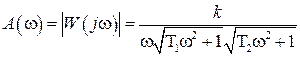 ,
,
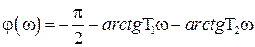 .
.
АФЧХ пересекает отрицательную полуось при 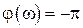 , что дает значение частоты
, что дает значение частоты 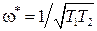 . При этой частоте модуль АЧХ будет равен
. При этой частоте модуль АЧХ будет равен 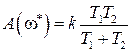 . В системе невозможны периодические режимы, если
. В системе невозможны периодические режимы, если 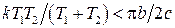 , т.е. при
, т.е. при
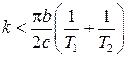 .
.
Если последнее неравенство не выполняется, то в системе возможны два периодических режима с амплитудами 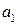 и
и 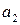 ,
, 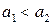 , как показано на рис. 2.18. Амплитуды
, как показано на рис. 2.18. Амплитуды 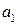 и
и 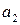 определяются из решения уравнения
определяются из решения уравнения
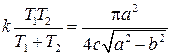 .
.
Применяя предложенный выше критерий устойчивости периодического режима, приходим к выводу, что режим с частотой 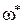 и амплитудой
и амплитудой 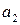 будет устойчивым, т.е. в системе возникнут автоколебания.
будет устойчивым, т.е. в системе возникнут автоколебания.
Дата добавления: 2015-02-07; просмотров: 1458;
