Теоремы Ляпунова

Кроме определений Ляпуновым были разработаны два метода анализа устойчивости решений дифференциальных уравнений.

Суть первого метода заключается в замене нелинейной системы (2.70) линейной (линеаризованной) путем разложения правых частей уравнений (2.70) в ряды Тейлора относительно начала координат 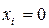и отбрасывания всех нелинейных членов. В результате получаются линейные уравнения (уравнения первого приближения)

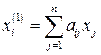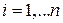, , (2.71)

где 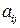− постоянные коэффициенты.

Ляпуновым доказана следующая основная теорема первого метода, которую приведем в упрощенной форме: если линейная система (2.71) асимптотически устойчива, то положение равновесия нелинейной системы (2.70) будет асимптотически устойчивым в малом, если система (2.71) неустойчива, то положение равновесия (2.70) будет неустойчивым.

По первому методу, исключая так называемые критические случаи, задача анализа устойчивости нелинейной системы сведена к более простой задаче анализа линейной системы. Первый метод Ляпунова не позволяет исследовать устойчивость в большом, целом или абсолютную устойчивость. Для этих целей Ляпуновым был разработан второй метод или прямой метод анализа устойчивости.

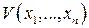
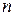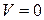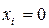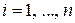Введем в рассмотрение непрерывную функцию переменных, такую, что при , , т.е. обращающуюся обязательно в ноль в начале координат.

Если в некоторой области переменных 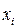функция 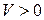или 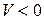, то ее называют знакоопределенной: соответствен положительно определенной или отрицательно определенной. Если функция 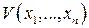сохраняет свой знак, но может обращаться в ноль не только в начале координат, то ее называют знакопостоянной (положительной или отрицательной). Такие функции в дальнейшем будем называть функциями Ляпунова. Примеры функций: 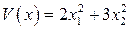− положительно определенная; 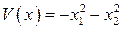− отрицательно определенная; 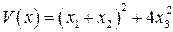− знакопостоянная функция (положительная).

Наконец, функция 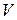называется знакопеременной, если в рассматриваемой области она меняет свой знак. Например, .

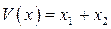Приведем три основные теоремы Ляпунова второго метода.

1. Если для системы уравнений (2.70) существует знакоопределенная функция 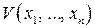, производная которой 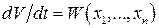является знакопостоянной противоположного знака, то решение 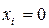устойчиво.

2. Если в предыдущем случае производная 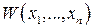будет знакоопределенной, но противоположного знака, то решение 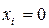будет устойчивым асимптотическим.

3. Если для системы уравнений (2.70) существует функция 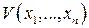, производная которой 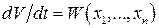является знакоопределенной функцией, причем в любой сколь угодно малой окрестности начала координат, имеется область, в которой знак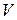и и 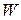совпадают, то решение 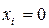системы (2.70) неустойчиво.

Отметим, что приведенные в теоремах условия являются только лишь достаточными и эффективность их будет зависеть от выбранной функции Ляпунова 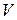. Не существует в общем случае методик выбора функций Ляпунова, дающих необходимые и достаточные условия.

Довольно часто в качестве функций Ляпунова используют квадратичные формы, для которых, используя известные критерии, можно сравнительно легко определять их знак.