Применение теоремы Гаусса для расчета напряженности электростатического поля

1. Поле равномерно заряженной бесконечной плоскости с поверхностной плотностью зарядов +s.

Пусть поверхностная плотность зарядов или заряд, приходящийся на единицу поверхности 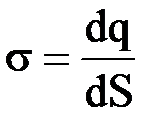. Силовые линии поля перпендикулярны этой плоскости и направлены от нее в обе стороны (рис.1.10).

Построим замкнутую цилиндрическую поверхность с основаниями dS, параллельными заряженной поверхности и образующей, параллельной вектору 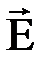. Следуя последнему условию, поток напряженности Ф_Е через боковую поверхность цилиндра равен нулю. Поэтому полный поток через цилиндрическую поверхность равен сумме потоков сквозь его основания. Так как вектор 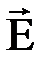перпендикулярен основаниям, Е_n=Е и суммарный поток Ф_Е можно записать Ф_Е=2ЕdS.

Рисунок 1.10 - Определение на­пряженности поля беско­нечной заряженной плос­кости.

Согласно теореме Гаусса 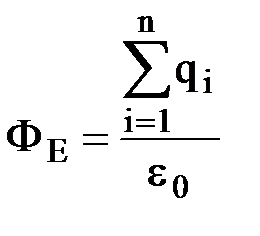, где 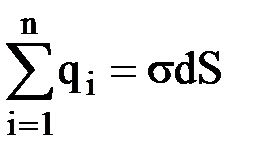- заряд, охватываемый цилиндрической по­верхностью. Таким образом ,

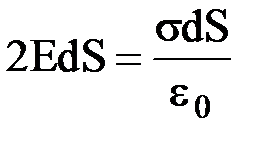отсюда .

Если плоскость помещена в среду с относительной ди­электрической проницаемостью e, то напряженность электростатического поля, соз­даваемая плоскостью, равна 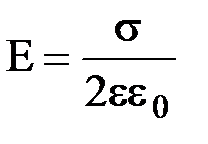. Из формулы следует, что Е не зависит от расстояния между плоскостью и точкой на­блюдения, т.е. поле равномерно заряженной бесконечной плоскости однородно.