Поле двух бесконечных разноименно заряженных плоскостей.

Рисунок 1.11 - Определение на­пряженности поля двух параллельных разноимен­но заряженных плоско­стей.

На рис.1.11 перпендикулярно чертежу располо­же­ны две такие плоскости с поверхностными плотно­стями за­рядов +s и -s. Силовые линии плоскостей перпенди­ку­лярны им и параллельны между собой. Силовые ли­нии выходят из плоскости +s и входят в плоскость ‑s. На ри­сунке сплошными стрелками изо­бражено поле плоскости +s и пунктирными - поле плоскости -s. Напряженности полей обеих плоскостей равны по абсолютной величине 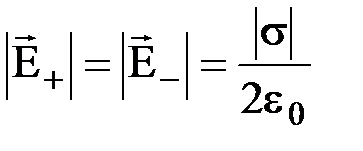. Однако, справа и слева от плоскостей напряженност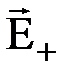и и 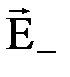направлены проти­во­положно, поэтому суммарная Е=0 и поле отсутствует. 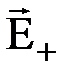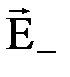В области между плоскос­тями и направлены одинаково, поэтому .

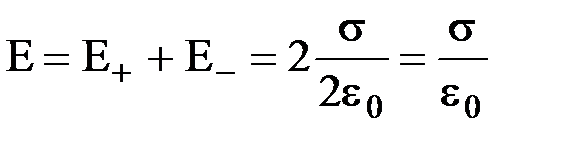3. Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R собщим зарядом Qзаряжена равномерно с поверхностной плотностью + s. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально (рис. 1.12).

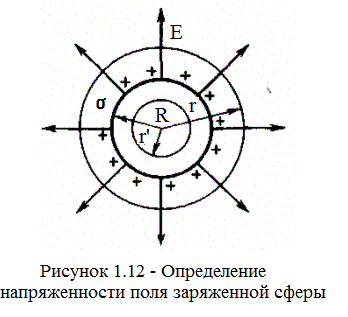
Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если г > R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса

4pr²E = Q/e₀,откуда

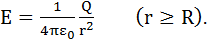
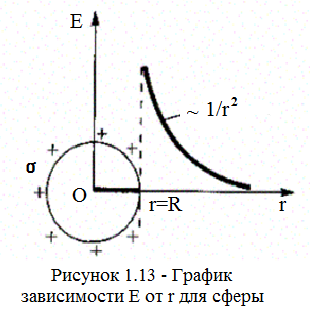При r>Rполе убывает с расстоянием rпо такому же закону, как у точечного заряда. График зависимости E от г приведен на рис. 1.13. Если r¢ < R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует

(Е = 0).

4.Поле объемно заряженного шара. Шар радиуса R собщим зарядом Qзаряжен равномерно с объемной плотностью r ( 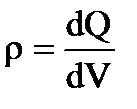- заряд, приходящийся на единицу объема).

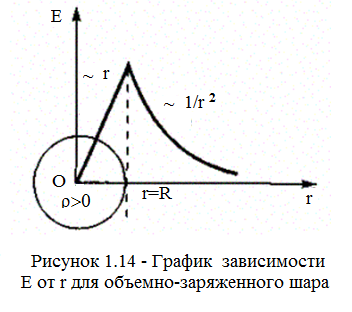
Учитывая соображения симметрии, можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае. Внутри же шара напряженность поля будет другая. Сфера радиуса r' < Rохватывает заряд Q' = 4/3pr¢³r. Поэтому, согласно теореме Гаусса,

4pr¢²E=Q¢/e₀=4/3pr¢³r/ e₀

Учитывая, что 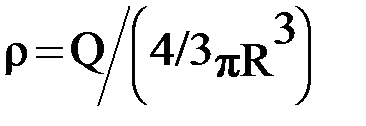, получаем

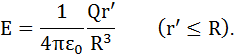
График зависимости Е от гдля рассмотренного случая приведен на рис. 1.14.

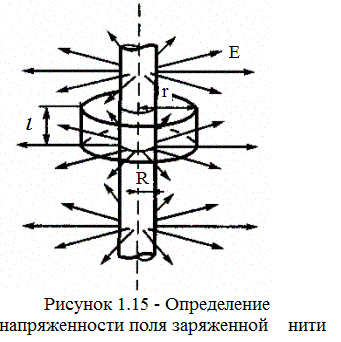5. Поле равномерно зараженного бесконечного цилиндра (нити). Бесконечный цилиндр радиуса R(рис. 1. 15) заряжен равномерно с линейной плотностью t ( 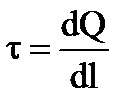- заряд, приходящийся на единицу длины).

Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса rи высотой l. Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность равен 2prlE. По теореме Гаусса при r > R 2prlE = tl/e₀, откуда

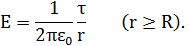
Если г < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области E = 0.

Контрольные вопросы первого уровня

1. Что такое точечный заряд? Сформулировать закон Кулона в вакууме. Чему равен коэффициент пропорциональности в законе?

2. Какое поле называется электростатическим? Что такое пробный заряд?

3. Что называется напряженностью поля, в чем измеряется напряженность поля, куда направлен вектор напряженности поля? Чему равна напряженность поля точечного заряда?

4. Что называется силовыми линиями, нарисуйте их для положительного заряда. Могут ли пересекаться силовые линии? Почему? Нарисовать силовые линии для отрицательного заряда. Что можно сказать о густоте силовых линий? Нарисовать силовые линии однородного и неоднородного поля.

5. Что называется электрическим диполем, плечом диполя, дипольным моментом?

6. Что называется поверхностной плотностью заряда? В чем измеряется? Что называется линейной плотностью заряда? Что называется объемной плотностью заряда?

7. Сформулируйте принцип суперпозиции полей.

8. Сформулировать закон сохранения заряда. Какова единица измерения заряда?

9. Что называется потоком напряженности электростатического поля? Сформулируйте теорему Остроградского-Гаусса для электрического поля в вакууме.

10. Чему равна напряженность поля сферы?

Методические указания по решению задач

Задачи электростатики можно разбить на два типа. К первому типу относятся задачи, в которых по заданному распределению зарядов в пространстве требуется найти напряженности и потенциалы созданных ими полей. Ко второму типу — задачи, в которых характеристики поля (потенциалы и напряженности) известны, и нужно найти величины зарядов, создающих это поле.

Если в задаче речь идет о точечных зарядах, то их решение основано на законе Кулона и законе сохранения заряда. Такие задачи рекомендуется решать в следующем порядке.

1.Указать силы, действующие на заряд, помещенный в электростатическое поле, и записать для заряда уравнение равновесия или основное уравнение динамики материальной точки.

2. Выразить силы электростатического взаимодействия через заряды и характеристики поля и подставить эти выражения в исходные уравнения.

3. Если при взаимодействии заряженных тел между ними происходит перераспределение зарядов, к составленному уравнению следует добавить закон сохранения заряда.

Проводя вычисления в задачах электростатики, полезно

помнить, что

.

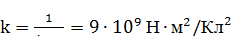4.Записать вспомогательные формулы и полученную систему уравнений решить относительно неизвестной величины.

Особое внимание следует обращать на векторный характер напряженности 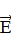поля и помнить, что знак потенциала определяется знаком заряда, создающего поле.

Если заряд, создающий поле, нельзя считать точечным, его всегда можно представить в виде совокупности элементарных (точечных) зарядов. Для каждого элементарного заряда справедливы закон Кулона и формулы для напряженности и потенциала поля точечного заряда. Поле таких зарядов может быть определено путем суммирования кулоновских полей, создаваемых каждым из элементарных зарядов в отдельности. Такого рода непосредственное суммирование не всегда возможно, так как требует в каждом отдельном случае довольно сложных вычислений.

Во многих задачах о нахождении напряженности поля протяженного заряда решение может быть выполнено с использованием теоремы Гаусса или теоремы о циркуляции вектора .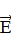

При решении задач электростатики нужно иметь в виду следующее.

1. Положительные электрические заряды, предоставленные самим себе, движутся в электростатическом поле от точек с большим потенциалом к точкам, где потенциал меньше. Отрицательные заряды движутся в противоположном направлении.

2. Электростатическое поле внутри статически заряженного проводника равно нулю. Этот результат не зависит от того, находится ли проводник во внешнем электрическом поле или нет. Потенциал всех точек, лежащих на проводнике, имеет при этом одинаковое значение, т. е. поверхность проводника является эквипотенциальной. Потенциал во всех точках внутри проводника равен потенциалу на его поверхности.

3. При внесении диэлектрика в электрическое поле модуль вектора напряженности 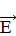уменьшается в ε раз в пространстве, занятом диэлектриком, и остается без изменения во всех остальных точках.

4. Потенциал Земли и всех тел, соединенных с Землей, принимается равным нулю.

5. Работа сил электростатического поля по замкнутому пути равна нулю.

6. Электрическое поле заряженного плоского конденсатора можно рассматривать как результат наложения двух полей, созданных каждой пластиной конденсатора.

7. Если плоский конденсатор подключить к источнику питания, зарядить его и потом отключить, то при изменении емкости конденсатора вследствие изменения расположения его пластин или внесения (удаления) диэлектрика заряд на конденсаторе не меняется.

8. Если конденсатор подключен к источнику постоянного напряжения, то при любых изменениях емкости конденсатора напряжение между его пластинами остается неизменным.

Цель: Расчет напряженности электростатического поля с помощью принципа суперпозиции полей и теоремы Гаусса.

Основные формулы

По закону Кулона сила электростатического взаимодействия между двумя заряженными телами, размеры которых малы, по сравнению с расстоянием r между ними, определяется формулой

,

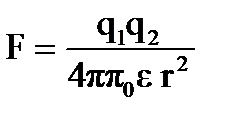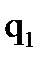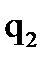где и - электрические заряды тел, ε – относительная диэлектрическая проницаемость среды, ε₀= 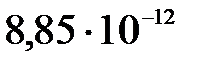Ф/м – электрическая постоянная.

Напряженность электрического поля определяется формулой

,

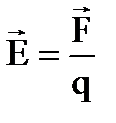где 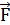– сила, действующая на заряд q. Напряженность поля точечного заряда

.

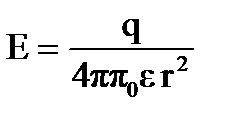По теореме Гаусса поток вектора напряженности сквозь любую замкнутую поверхность ,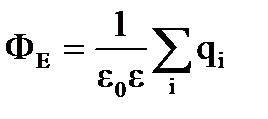

где 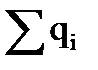- алгебраическая сумма зарядов, находящихся внутри этой поверхности. При помощи теоремы Гаусса можно найти напряженность электрического поля, образованного различными заряженными телами.

Напряженность поля, образованного заряженной бесконечно длинной нитью, ,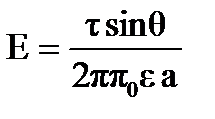

где 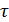- линейная плотность заряда на нити, а- расстояние от нити.

Напряженность поля, образованного заряженной бесконечной плоскостью, ,

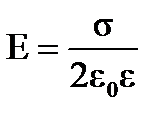где σ– поверхностная плотность заряда на плоскости.

Напряженность поля плоского конденсатора

.

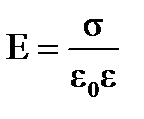Напряженность поля, образованного заряженным шаром,

,

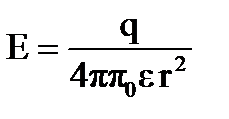где q- заряд шара радиусом R, r- расстояние от центра шара, причем r≥R.