Примеры решения задач. Задача 1.Два одинаковых шарика, несущих равные заряды, подвешены на нитях равной длины к одной точке
Задача 1.Два одинаковых шарика, несущих равные заряды, подвешены на нитях равной длины к одной точке. Шарики опускают в керосин. Чему равна плотность материала шариков, если угол расхождения нитей в воздухе и в керосине одинаков? Плотность керосина ρк=0,8 г/см3, его диэлектрическая проницаемость ε = 2.
Решение: Когда система находится в воздухе, то на каждый шарик действует три силы (Рис.1.16 а): сила тяжести m
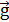 сила натяжения нити
сила натяжения нити 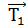 и кулоновская сила
и кулоновская сила 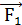 . Так как шарики находятся в равновесии, то сумма сил равна нулю:
. Так как шарики находятся в равновесии, то сумма сил равна нулю:
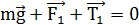 .
.
Это означает, что при сложении сил векторы образуют прямоугольный треугольник (Рис.1,16. б). Из этого треугольника имеем: F1 = mg tgα
Рисунок 1.16. К задаче 1 При погружении в керосин появляется
ещё архимедова сила Fa, а сила натяжения нити T2 и кулоновская сила F2 уменьшаются по модулю. Шарики находятся в равновесии, значит,
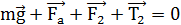 .
.
Отсюда следует, что
F2 = (mg – Fa) tgα.
Отношение модулей сил и есть диэлектрическая проницаемость среды:
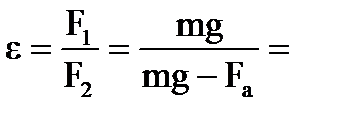
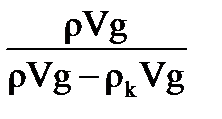 .
.
Отсюда
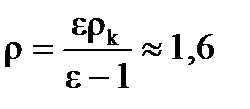 г/см3.
г/см3.
Задача 2. В атоме водорода электрон движется по стационарной круговой орбите с угловой скоростью 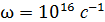 . Определите радиус орбиты. Заряд электрона е=1,6
. Определите радиус орбиты. Заряд электрона е=1,6 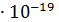 Кл, его масса m=9,1
Кл, его масса m=9,1 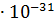 кг.
кг.
Решение: В простейшей модели атома водорода считается, что электрон с зарядом -е движется по круговой орбите вокруг положительно заряженного ядра с зарядом +е. На электрон действует кулоновская сила притяжения к ядру F. Силой тяжести электрона можно пренебречь, так как она намного меньше F.
По второму закону Ньютона
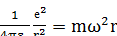 ,
,
Откуда
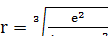 =1,4
=1,4 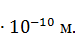
Задача 3.В сильном однородном электрическом поле напряженностью 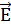 на одной силовой линии в точках 1и 2, расположенных на расстоянии l0друг от друга, находятся протон р и электрон е. Начальная скорость обеих частиц равна нулю. Чему равно расстояние между частицами спустя время τпосле начала движения?
на одной силовой линии в точках 1и 2, расположенных на расстоянии l0друг от друга, находятся протон р и электрон е. Начальная скорость обеих частиц равна нулю. Чему равно расстояние между частицами спустя время τпосле начала движения?
 Решение: Направим ось Хпо направлению силовой линии
Решение: Направим ось Хпо направлению силовой линии 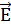 , а начало отсчета совместим с точкой 2, где вначале находился электрон. Пренебрегая взаимодействием частиц друг с другом (сильное поле), можно считать движение электрона и протона равноускоренным. Тогда координата протона в момент времени τ равна:
, а начало отсчета совместим с точкой 2, где вначале находился электрон. Пренебрегая взаимодействием частиц друг с другом (сильное поле), можно считать движение электрона и протона равноускоренным. Тогда координата протона в момент времени τ равна:
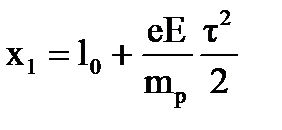 , Рисунок 1.17.
, Рисунок 1.17.
где е- заряд, mр- масса протона. К задаче 3
Координата электрона 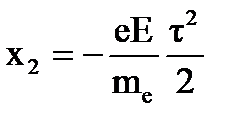 ,
,
где mе- масса электрона. Искомое расстояние
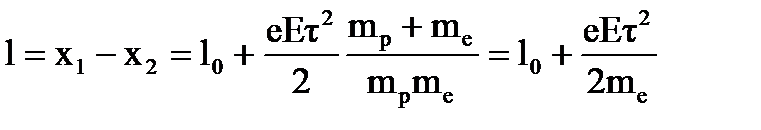 ,
,
так как mрмного больше mе.
Задача 4. В вершинах квадрата со стороной a расположены два положительных и два отрицательных заряда, значение каждого из них Q (Рис.1.18 а, б). Определить напряжённость электрического поля в центре этого квадрата.
Решение: Поле создано четырьмя точечными зарядами. Поэтому напряжённость следует определять с помощью принципа суперпозиции:
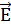 =
= 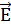 1+
1+ 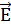 2+
2+ 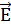 3
3 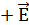 4.
4.
Сначала следует показать на рисунке направление всех векторов
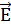 i зависящее от знака заряда Qi.
i зависящее от знака заряда Qi.
Рисунок 1.18. К задаче 4
Расстояние от любого из зарядов до рассматриваемой точки
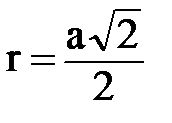 .
.
Рассмотрим распределение зарядов, показанное на рисунке 1.18 а. Напряжённости 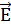 2 и
2 и 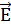 4 полей, созданных вторым и четвёртым зарядами в точке С, сонаправлены и равны по модулю: E2=E4. Аналогично,E1=E3. Поэтому напряженность результирующего поля
4 полей, созданных вторым и четвёртым зарядами в точке С, сонаправлены и равны по модулю: E2=E4. Аналогично,E1=E3. Поэтому напряженность результирующего поля
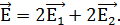
Векторы 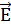 1 и
1 и 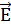 2 также равны по модулю и направлены ортогонально друг другу (по диагоналям квадрата), значит, результирующий вектор
2 также равны по модулю и направлены ортогонально друг другу (по диагоналям квадрата), значит, результирующий вектор 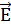 направлен вертикально вниз и тогда
направлен вертикально вниз и тогда
E = 4E1 cos 45o.
Напряженность поля, созданного каждым из зарядов,
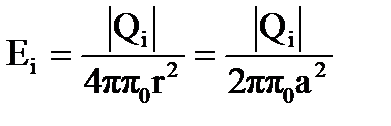
Заряд Qi следует брать по модулю, так как знак каждого из зарядов был учтён при изображении соответствующего вектора 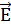 i. Окончательно
i. Окончательно
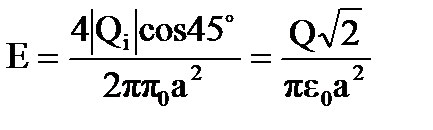 .
.
При расположении зарядов, показанном на рисунке 1.19 б, Е = 0.
Задача 5.Кольцо из проволоки радиусом R= 10 см имеет отрицательный заряд q = -5нКл. Найти напряжённости Е электрического поля на оси кольца в точках, расположенных от центра кольца на расстояниях L, равных 0, 5, 8, 10 и 15см. Построить график E = f(L). На каком расстоянии от центра кольца напряжённость Е электрического поля будет иметь максимальное значение?
Решение. Возьмем элемент кольца dl. Этот элемент имеет заряд dq. Напряженность электрического поля, заданная этим элементом в точке А, будет 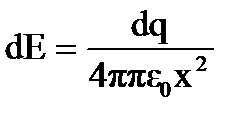 .
.
Вектор 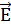 направлен по линии x, соединяющей точку А с элементом кольца dl (рис.1.19). Для нахождения напряженности поля всего кольца надо векторно сложить
направлен по линии x, соединяющей точку А с элементом кольца dl (рис.1.19). Для нахождения напряженности поля всего кольца надо векторно сложить 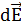 от всех элементов. Вектор d
от всех элементов. Вектор d 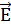 можно разло- жить на две составляющие d
можно разло- жить на две составляющие d 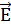 n и d
n и d 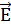 τ. Составляющие d
τ. Составляющие d 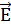 n каждых двух диаметрально расположенных элементов взаимно уничтожаются, поэтому
n каждых двух диаметрально расположенных элементов взаимно уничтожаются, поэтому 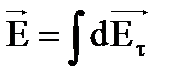 . Но dEτ=dEcosα=
. Но dEτ=dEcosα= 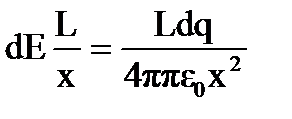 , что дает Рисунок 1.19. К задаче 5
, что дает Рисунок 1.19. К задаче 5 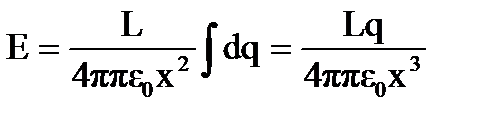 .Учитывая, что
.Учитывая, что 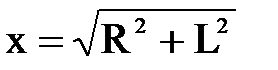 , имеем
, имеем
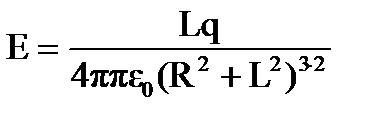 (1)
(1)
Если L>>R, то 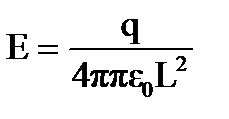 , т.е. на больших расстояниях заряженное кольцо можно рассматривать как точечный заряд.
, т.е. на больших расстояниях заряженное кольцо можно рассматривать как точечный заряд.
Выразим величины x и L через угол α. Имеем R = x sinα, L = x cos α; теперь формула (1) примет вид 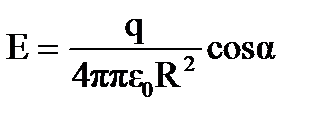 sin2α. Для нахождения максимального значения напряженности Е возьмем производную
sin2α. Для нахождения максимального значения напряженности Е возьмем производную 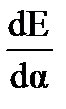 и приравняем ее к нулю:
и приравняем ее к нулю: 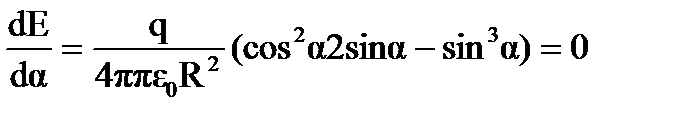 или tg2α = 2. Тогда напряженность электрического поля имеет максимальное значение в точке А, расположенной на расстоянии
или tg2α = 2. Тогда напряженность электрического поля имеет максимальное значение в точке А, расположенной на расстоянии 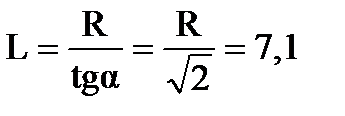 см от центра кольца. Подставляя в (1) числовые данные, составим таблицу и построим график.
см от центра кольца. Подставляя в (1) числовые данные, составим таблицу и построим график.
| L, м | 0,05 | 0,08 | 0,1 | 0,15 | |
| E, В/м |

Задача 6.На некотором расстоянии от бесконечной равномерно заряженной плоскости плотностью σ= 0,1 нКл/см2 положена круглая пластинка. Плоскость пластинки составляет с линиями напряженности угол 30о. Определите поток ФЕ вектора напряженности через эту пластинку, если ее радиус r равен 15 см.
Решение. Поток вектора напряженности ФЕ через пластинку площадью равен
ФЕ = E S cosα.
Напряженность электростатического поля, создаваемого заряженной плоскостью (рис.1.20) с поверхностной плотностью заряда σ:
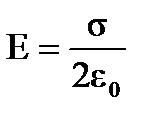 .
.
Площадь пластинки S = πr2, где r – Рисунок 1.20. К задаче 6 радиус пластинки.
Угол α, образуемый нормалью к пластинке  и вектором
и вектором 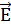 равен 60о. Следовательно,
равен 60о. Следовательно,
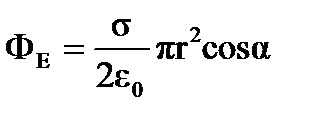 .
.
Вывод: Напряженность 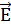 является силовой характеристикой электрического поля. Она определяется зарядом – источником данного электрического поля и не зависит от пробного заряда q, внесенного в это поле. Очень важно определить правильно какой заряд является пробным, а какой является источником поля.
является силовой характеристикой электрического поля. Она определяется зарядом – источником данного электрического поля и не зависит от пробного заряда q, внесенного в это поле. Очень важно определить правильно какой заряд является пробным, а какой является источником поля.
Контрольные вопросы второго уровня (сборник задач).
1. Три одинаковых положительных заряда q1=q2=q3=1 нКл расположены по вершинам равностороннего треугольника. Какой отрицательный заряд q4 нужно поместить в центре треугольника, чтобы сила притяжения с его стороны уравновесила силы взаимного отталкивания зарядов, находящихся в вершинах? [0,58 нКл]
2. Даны два шарика массой m=1 г каждый. Какой заряд q нужно сообщить каждому шарику, чтобы сила взаимного отталкивания зарядов уравновесила силу взаимного притяжения шариков по закону тяготения? Рассматривать шарики как материальные точки. [86,7 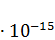 Кл]
Кл]
3. Два шарика массой m=0,1 г каждый подвешены в одной точке на нитях длиной l=20 см каждая. Получив одинаковый заряд, шарики разошлись так, что нити образовали между собой угол α=60  . Найти заряд каждого шарика. [50,1 нКл]
. Найти заряд каждого шарика. [50,1 нКл]
4. Два одинаковых проводящих заряженных шара находятся на расстоянии r =60 см. Сила отталкивания F1 шаров равна 70 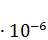 Н. После того как шары привели в соприкосновение и удалили друг от друга на прежнее расстояние, сила отталкивания возросла и стала равной F2 =1,6
Н. После того как шары привели в соприкосновение и удалили друг от друга на прежнее расстояние, сила отталкивания возросла и стала равной F2 =1,6 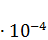 Н. Вычислить заряды q1 и q2, которые были на шарах до их соприкосновения. Диаметр шаров считать много меньшим расстояния между ними. [0,14 мкКл; 20 нКл]
Н. Вычислить заряды q1 и q2, которые были на шарах до их соприкосновения. Диаметр шаров считать много меньшим расстояния между ними. [0,14 мкКл; 20 нКл]
5. Определите напряженность E поля, создаваемого зарядом, равномерно распределенным по тонкому прямому стержню с линейной плотностью τ = 200 нКл/м, в точке, лежащей на продолжении оси стержня на расстоянии а = 20 см от ближайшего конца. Длина стержня l = 40 см. [6 кВ/м]
6. С какой силой, приходящейся на единицу площади, отталкиваются две одноименно заряженные бесконечно протяженные плоскости с одинаковой поверхностной плотностью заряда σ = 2 мкКл /м2? [0,23 Па]
7. Определите угловую скорость вращения четырех зарядов -q массой m, расположенных в углах квадрата со стороной d, движущихся по круговым орбитам. Центры орбит совпадают с центром квадрата. В центре квадрата расположен заряд +q. Взаимное расположение зарядов при движении не изменяется. [ 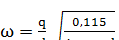 ]
]
8. Тонкая бесконечная нить согнута под углом 90°. Нить несет заряд, равномерно распределенный с линейной плотностью τ = 1 мкКл/м. Определите силу, действующую на точечный заряд q = 0,1 мкКл, расположенный на продолжении одной из сторон и удаленный от вершины угла на а = 50 см. [4 мН]
9. Тонкое полукольцо радиусом R=10 см несет равномерно распределенный заряд с линейной плотностью τ = 1 мкКл/м. В центре кривизны полукольца находится положительный точечный заряд, взаимодействующий с полукольцом с силой 3,6 мН. Найдите величину точечного заряда. [20 нКл]
10. Три одинаковых точечных заряда q1 = q2=q3= 2 нКл находятся в вершинах равностороннего треугольника со стороной a = 10 см. Определите модуль и направление силы F, действующей на один из зарядов со стороны двух других. [3,6 мН]
11. Четыре одинаковых заряда q1 = q2 = q3 = q4 = 40 нКл закреплены в вершинах квадрата со стороной a = 10 см. Найдите силу F, действующую на один из этих зарядов. [2,75 мН]
12. На расстоянии d = 20 см находятся два точечных заряда q1 = -50 нКл и q2 = 100 нКл. Определите силу F, действующую на заряд q3 = -10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d. [0,195 мН]
13. Расстояние dмежду двумя точечными зарядами q1 = 2 нКл и q2 = 4 нКл равно 60 см. Определите точку, в которую нужно поместить третий заряд q3 так, чтобы система зарядов находилась в равновесии. Определите размер и знак заряда. Устойчивое или неустойчивое будет равновесие? [-0,7 нКл; 0,246 м от меньшего заряда]
14. На тонком кольце равномерно распределен заряд с линейной плотностью τ = 0,2 нКл/см. Радиус кольца R = 15 см. На срединном перпендикуляре к плоскости кольца находится точечный заряд q= 10 нКл. Определите силу F, действующую на точечный заряд со стороны заряженного кольца, если он удален от центра кольца на: 1) а, = 20 см; 2)a2=10 м. [1)1,6 мкН; 2)0,017 мкН]
15. По тонкой нити, изогнутой по дуге окружности радиусом R = 10 см, равномерно распределен заряд q = 20 нКл. Определите напряженность Е поля, создаваемого этим зарядом в точке, совпадающей с центром кривизны дуги, если длина нити равна четверти длины окружности. [16 кВ/м]
16. Два длинных тонких равномерно заряженных (τ = 1 мкКл/м) стержня расположены перпендикулярно друг другу так, что точка пересечения их осей находится на расстоянии a= 10 см и b= 15 см от ближайших концов стержней. Найдите силу F, действующую на заряд q = 10 нКл, помещенный в точку пересечения осей стержней. [0,1 мкН]
17. Параллельно бесконечной плоскости, заряженной с поверхностной плотностью σ=4 мкКл/м2, расположена бесконечно длинная прямая нить, заряженная с линейной плотностью τ=100 нКл/м. Определите силу F, действующую со стороны плоскости на отрезок нити длиной l=1 м. [2,26 пН]
18. Две одинаковые круглые пластины площадью S = 400 см2 каждая расположены параллельно друг другу. Заряд одной пластины q1 = 400 нКл, другой q2= -200 нКл. Определите силу F взаимного притяжения пластин, если расстояние между ними: а) r1 = 3 мм; б) r2 = 10 м. [а) 0,113 Н; б) 7,2 мкН]
19. На бесконечном тонкостенном цилиндре диаметром d = 20 см равномерно распределен заряд с поверхностной плотностью σ = 4 мкКл/м2. Определите напряженность поля в точке, отстоящей от поверхности цилиндра на а = 15 см. [129 кВ/м]
20. Две длинные прямые параллельные нити находятся на расстоянии d= 5 см друг от друга. На нитях равномерно распределены заряды с линейными плотностями τ1 = -5 нКл/см и τ2= 10 нКл/см. Определите напряженность Е электрического поля в точке, удаленной от первой нити на расстояние r1 = 3 см и от второй на расстояние r2 = 4см. [54 В/м]
21. К бесконечной равномерно заряженной вертикальной плоскости подвешен на нити одноименно заряженный шарик массой m = 50 мг и зарядом q = 0,6 нКл. Сила натяжения нити, на которой висит шарик, F= 0,7 мН. Найдите поверхностную плотность заряда σ на плоскости. [20,6 мкКл/м2]
22. С какой силой (на единицу длины) взаимодействуют две заряженные бесконечно длинные параллельные нити с одинаковой линейной плотностью заряда τ = 20 мкКл/м, находящиеся на расстоянии R = 10 см друг от друга? [72 Н/м]
23. Бесконечная плоскость несет заряд, равномерно распределенный с поверхностной плотностью σ = 1 мкКл/м2. На некотором расстоянии от плоскости, параллельно ей, расположен круг радиусом r = 10 см. Вычислите поток вектора напряженности через этот круг. [1,78 кВ • м)
24. В центре сферы радиусом r =20 см находится точечный заряд q = 10 нКл. Определите поток вектора напряженности через часть сферической поверхности площадью S=20 см2. [4,5 В  м]
м]
25. В вершинах конуса с раствором телесного угла Ω = 0,5 стер находится точечный заряд q = 30 нКл. Вычислите поток вектора напряженности через площадку, ограниченную линией пересечения поверхности конуса с любой другой поверхностью. [135 В • м]
26. Прямоугольная плоская площадка со сторонами а = 3 см и b = 2 см находится на расстоянии r = 1 м от точечного заряда q = 1 мкКл. Площадка ориентирована так, что линии напряженности составляют угол α = 30° с ее поверхностью. Найдите поток вектора напряженности через площадку. [2,7 В  м]
м]
27. Электрическое поле создано точечным зарядом q = 0,1 мкКл. Определите поток вектора напряженности через круглую пластинку радиусом r =30 см. Заряд равноудален от краев площадки и находится на расстоянии а = 40 см от ее центра. [1,13 кВ  м]
м]
28. Электрическое поле создано бесконечной прямой, равномерно заряженной нитью (τ = 0,3 мкКл/м). Определите поток вектора напряженности через прямоугольную площадку, две большие стороны которой параллельны заряженной нити и одинаково удалены от нее на расстояние r=20 см. Стороны площадки имеют размеры а = 20 см, b = 40 см. [ 1,08 кВ  м ]
м ]
29. Точечный заряд q расположен в центре куба со стороной d. Чему равен поток вектора напряженности через одну грань куба? [q/(6ε0)]
30. Заряд qпомещен в один из углов куба. Чему равен поток вектора напряженности через каждую из граней куба? [q/(24ε0), 0]
Контрольные вопросы третьего уровня (тесты)
1. Какое из приведенных ниже выражений есть определение напряженности электрического поля?
| а)E =; | б) ÑЕ = ; | в)E =; |
| г) E = ; | д)E = . |
2. Установите соответствие между определением физической величины и его математическим выражением.
| Определение | Математическое выражение | ||
| а) линейная плотность заряда | 1) r = | ||
| б) поверхностная плотность заряда | 2) l = | ||
| в) объемная плотность заряда | 3) s = | ||
| а) ; | б) ; | в) . | |
3. Напряженности электрического поля заряженного тела поставьте в соответствие математическое выражение.
| Напряженность электрического поля | Математическое выражение | ||||
| а) точечного заряда на расстоянии r | 1) E = | ||||
| б) внутри объемно-заряженного шара | 2) E = | ||||
| в) бесконечно длинной равномерно заряженной нити на расстоянии r от ее оси | 3) E = | ||||
| г) бесконечной равномерно заряженной плоскости | 4) E = | ||||
| д) плоского конденсатора | 5) E= | ||||
| а) ; | б) ; | в) ; | г) ; | д) . | |
4. Как изменится по модулю напряженность электрического поля точечного заряда при уменьшении расстояния до заряда в 4 раза?
| а) уменьшится в 2 раза; | б) уменьшится в 4 раза; | в) уменьшится в 16 раз; |
| г) увеличится в 2 раза; | д) увеличится в 4 раза; | е) увеличится в 16 раз. |
5. Каково направление вектора напряженности электрического поля в точке О, созданного равными по модулю зарядами +q?
| · +q |
| О |
| · +q |
| · +q |
| · +q |
| · |
| a) 1; | б) 2; | в) 3; | г) 4; |
| д) напряженность в точке О равна нулю. |
6. В каких из четырех случаев различного распределения зарядов, приведенных ниже, напряженность электростатического поля в точке А равна нулю?
1) 2) 3) 4)
| а) 1, 2; | б) 2, 3; | в) 3; | г) 4; | д) 3, 4. |
7.
| II |
| I |
Вблизи равномерно заряженной нити мысленно построим замкнутую поверхность, имеющую форму цилиндра, соосного с нитью I. Как изменится модуль потока вектора напряженности электрического поля через ту же поверхность цилиндра, если нить наклонить (II), сохранив пересечение нити с основаниями цилиндра? Среда однородна.
| а) увеличится; | б) уменьшится; | в) не изменится. | |||||
| а) ; | б) ; | в) ; | г) ; | д) . | |||
8. Укажите, на каком графике правильно показана зависимость напряженности электростатического поля Е от расстояния r для тонкой равномерно заряженной бесконечной нити r?
а) б) в) г)
9. Укажите, на каком графике правильно показана зависимость напряженности электростатического поля Е от расстояния r для равномерно заряженной проводящей сферы радиусом R.
а) б) в) г)
10. Какой из приведенных ниже графиков отражает зависимость напряженности электростатического поля Е от расстояния r для равномерно заряженного по объему шара радиусом R?
а) б) в) г)
Дата добавления: 2015-02-13; просмотров: 13430;
