Коррекция нелинейной системы с помощью обратной связи

Рассмотрим метод подавления автоколебаний, основанный на введении обратной связи, охватывающей нелинейный элемент и часть линейной системы (рис. 2.22). Предполагается, что НЭ относится к статическому типу.

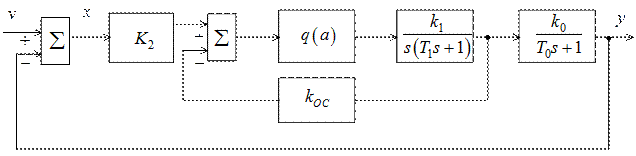
Рис. 2.22

Запишем характеристическое уравнение гармонически линеаризованной замкнутой системы:

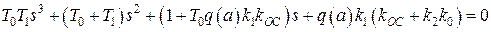, (2.75)

где 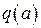– гармонически линеаризованный коэффициент усиления нелинейного элемента.

В соответствии с критерием устойчивости Гурвица система третьего порядка будет находиться на границе устойчивости при условии:

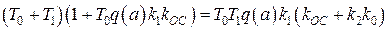. (2.76)

По данному выражению можно построить границу устойчивости системы в области интересующих параметров, задаваясь максимальным значением характеристики нелинейного элемента. Например, для идеального двухпозиционного реле 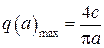, и тогда максимальное значение 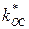, соответствующее границе устойчивости НСАУ, войдет в соотношения:

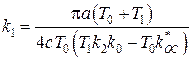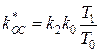, . (2.77)

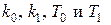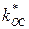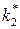Из (2.77) при известных значениях, например, находятся предельные значения и . Для обеспечения устойчивости НСАУ значения 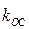и 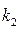должны быть выбраны так, чтобы они попали в область, соответствующую отсутствию автоколебаний.