Прохождение случайных сигналов через линейную непрерывную систему автоматического управления
При анализе САУ со случайными воздействиями необходимо оценить изменения характеристик случайных процессов при прохождении случайных сигналов через динамическую систему. Рассмотрим эту задачу в простейшем варианте, когда имеется сигнал 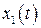 на входе системы (звена),
на входе системы (звена), 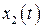 - на её выходе, а сама система описывается передаточной функцией
- на её выходе, а сама система описывается передаточной функцией 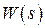 , т.е. является линейной. Будем полагать, что на входе системы действуют стационарные случайные сигналы с известными характеристиками: математическим ожиданием
, т.е. является линейной. Будем полагать, что на входе системы действуют стационарные случайные сигналы с известными характеристиками: математическим ожиданием 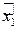 , дисперсией
, дисперсией 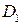 , корреляционной функцией
, корреляционной функцией 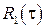 и спектральной плотностью
и спектральной плотностью  .
.
Далее предположим, что после затухания переходных процессов на выходе системы имеем установившиеся процессы (это предполагает асимптотически устойчивую систему), т.е. процесс на выходе будем считать стационарным случайным процессом. В этом случае основные характеристики стационарного случайного сигнала 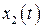 на выходе могут быть вычислены по формулам
на выходе могут быть вычислены по формулам
 , (3.9)
, (3.9)
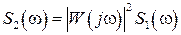 , (3.10)
, (3.10)
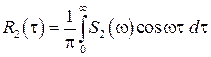 , (3.11)
, (3.11)
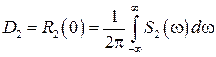 , (3.12)
, (3.12)
где 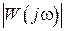 - амплитудно-частотная характеристика (АФЧХ), получаемая из
- амплитудно-частотная характеристика (АФЧХ), получаемая из 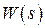 при
при 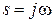 .
.
Для вычисления дисперсии 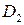 по выражению (3.12) разработаны специальные методы и таблицы.
по выражению (3.12) разработаны специальные методы и таблицы.
Отметим два частных важных случая, когда 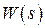 является передаточной функцией идеального дифференцирующего звена
является передаточной функцией идеального дифференцирующего звена 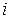 -го порядка
-го порядка 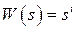 или идеального интегрирующего звена
или идеального интегрирующего звена 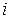 -го порядка
-го порядка 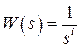 , тогда для первого случая
, тогда для первого случая 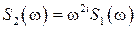 , а для второго
, а для второго 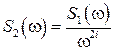 .
.
Рассмотрим анализ замкнутых линейных систем автоматического управления, стандартная структура для которых имеет вид, представленный на рис. 3.3.


Рис.3.3
Переменные 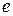 ,
,  и
и 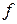 в области изображений связаны соотношениями
в области изображений связаны соотношениями
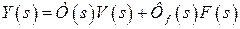 , (3.13)
, (3.13)
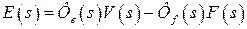 , (3.14)
, (3.14)
где главная передаточная функция замкнутой системы 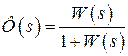 ;
;
передаточная функция замкнутой систем по возмущению 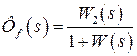 ; передаточная функция замкнутой системы по ошибке
; передаточная функция замкнутой системы по ошибке 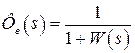 ;
;
передаточная функция разомкнутой системы 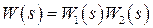 .
.
По передаточным функциям несложно найти АЧХ как 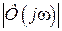 ,
, 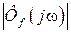 и
и 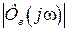 . Полагая входной сигнал
. Полагая входной сигнал  и возмущение
и возмущение 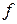 случайными стационарными процессами и задавая их характеристики
случайными стационарными процессами и задавая их характеристики 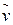 ,
, 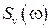 ,
,  ,
, 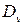 ,
, 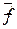 ,
, 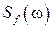 ,
, 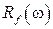 ,
, 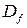 по формулам (3.9) – (3.12) можно получить характеристики случайных сигналов
по формулам (3.9) – (3.12) можно получить характеристики случайных сигналов 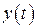 и
и 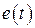 . При этом следует различать два случая, когда случайные сигналы
. При этом следует различать два случая, когда случайные сигналы 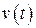 и
и 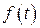 не коррелированны между собой и когда они коррелированны.
не коррелированны между собой и когда они коррелированны.
Если случайные сигналы некоррелированные, то, например, для первого соотношения (3.13) получим
 , (3.15)
, (3.15)
 , (3.16)
, (3.16)
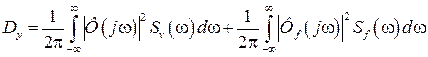 . (3.17)
. (3.17)
Аналогично можно получить характеристики случайного сигнала ошибки 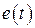 .
.
В случае коррелированных случайных сигналов 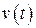 и
и 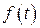 следует дополнительно знать их взаимные корреляционные функции
следует дополнительно знать их взаимные корреляционные функции 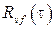 и
и  , а также взаимные спектральные плотности
, а также взаимные спектральные плотности 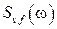 и
и 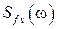 . При этом, например, в (3.17) появятся ещё два слагаемые, соответствующие спектральным плотностям
. При этом, например, в (3.17) появятся ещё два слагаемые, соответствующие спектральным плотностям 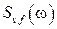 и
и 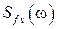 [6].
[6].
Приведенное выше касается вопросов анализа САУ, т.е. определения характеристик случайных процессов в самой системе при заданных структуре системы (рис. 3.3), передаточных функциях 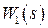 ,
, 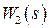 и характеристиках случайных сигналов
и характеристиках случайных сигналов 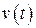 и
и 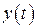 . Теоретически эта задача решается с использованием изложенных аналитических методов.
. Теоретически эта задача решается с использованием изложенных аналитических методов.
3.3. Расчёт точности системы при случайных воздействиях
Рассмотрим расчёт среднеквадратичной ошибки на примере системы, структурная схема которой имеет вид, изображённый на рис. 3.4.


Рис. 3.4
Пусть на вход системы поступают регулярный сигнал 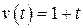 и помеха
и помеха 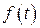 типа “белый шум” со спектральной плотностью
типа “белый шум” со спектральной плотностью 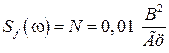 . Параметры передаточной функции:
. Параметры передаточной функции: 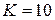 1/с,
1/с, 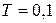 с.
с.
Необходимо определить среднеквадратичную ошибку. Средний квадрат ошибки  , где
, где 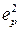 - квадрат регулярной составляющей ошибки, а
- квадрат регулярной составляющей ошибки, а  - средний квадрат случайной составляющей ошибки.
- средний квадрат случайной составляющей ошибки.
Составляющая  находится по известной формуле:
находится по известной формуле: 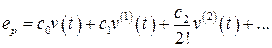 .
.
Коэффициенты ошибок  определяются при разложении в ряд Маклорена передаточной функции системы по ошибке
определяются при разложении в ряд Маклорена передаточной функции системы по ошибке 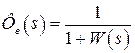 . В нашем случае
. В нашем случае  .
.
Так как 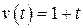 , то надо вычислить лишь первую производную
, то надо вычислить лишь первую производную  .
.
Следовательно  . При учёте численных значений
. При учёте численных значений  , а
, а  .
.
Определим среднее значение квадрата случайной составляющей  . Как показано в
. Как показано в 
 . (3.18)
. (3.18)
Для преодоления трудностей при вычислении интеграла (3.18), его представляют в виде:
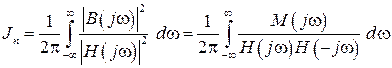 , (3.19)
, (3.19)
где  ;
; 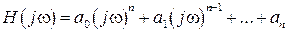 .
.
Формулы для вычисления интегралов по коэффициентам 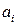 и
и 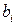 для соответствующих значений
для соответствующих значений 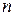 сведены в таблицы. Приведём их для
сведены в таблицы. Приведём их для 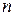 от 1 до 3
от 1 до 3 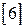 :
:
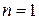 ;
; 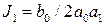 ;
;
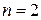 ;
; 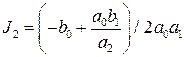 ;
;
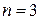 ;
; 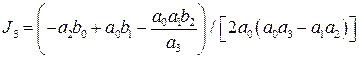 .
.
В нашем случае 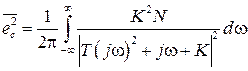 ;
;  ;
; 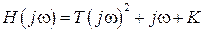 . Коэффициенты:
. Коэффициенты: 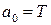 ,
, 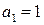 ,
, 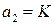 ,
, 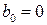 ,
, 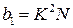 . Интеграл
. Интеграл 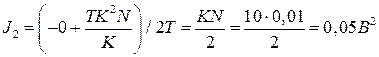 .
.
Среднеквадратичная ошибка 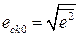 . С учётом численных значений
. С учётом численных значений 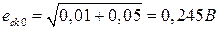 .
.
Дата добавления: 2015-02-07; просмотров: 1998;
