Случайные процессы в нелинейных системах
Нелинейные элементы искажают входные случайные сигналы. В связи с тем, что в НСАУ не применим принцип суперпозиции, при одновременном поступлении полезного сигнала и помехи влияние последней может существенно ослабить действие полезного сигнала и ухудшить качество функционирования системы. Поскольку общие точные методы исследования НСАУ со случайными воздействиями отсутствуют, прибегают к статистической линеаризации нелинейных элементов, что позволяет затем использовать известные методы расчёта линейных систем.
Рассмотрим кратко метод статистической линеаризации. Он основан на замене нелинейных преобразований статистически эквивалентными преобразованиями. На рис. 3.7 изображены нелинейный (НЭ) и линейный (ЛЭ) элементы.

Рис. 3.7
Процессы на входе и на выходе НЭ представляют в виде:
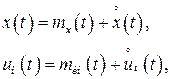 (3.32)
(3.32)
где 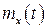 и
и  − математические ожидания, а
− математические ожидания, а 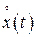 и
и 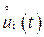 − центрированные (у которых матожидание равно 0) составляющие процессов
− центрированные (у которых матожидание равно 0) составляющие процессов 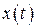 и
и 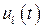 .
.
При статистической линеаризации нелинейное преобразование 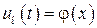 заменяют линейным вида:
заменяют линейным вида:
 . (3.33)
. (3.33)
Коэффициенты 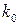 и
и 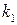 выбираются так, чтобы выполнялись определённые критерии статистической эквивалентности нелинейного и линейного преобразований.
выбираются так, чтобы выполнялись определённые критерии статистической эквивалентности нелинейного и линейного преобразований.
Первый критерий заключается в равенстве математических ожиданий и дисперсий процессов на выходе НЭ и ЛЭ. Второй связан с минимизацией среднего квадрата разности процессов на выходе этих элементов.
На основании первого критерия
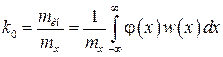 , (3.34)
, (3.34)
 . (3.35)
. (3.35)
Здесь 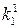 соответствует первому критерию эквивалентности.
соответствует первому критерию эквивалентности.
По второму критерию
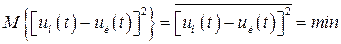 . (3.36)
. (3.36)
После преобразований уравнения (3.36) с учётом (3.32) и (3.33) и исследования на 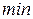
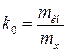 , (3.37)
, (3.37)
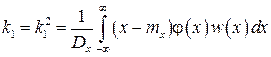 . (3.38)
. (3.38)
Из сопоставления выражений (3.37) и (3.34), а также (3.38) и (3.35) следует, что коэффициенты 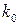 , найденные по различным критериям, совпадают а
, найденные по различным критериям, совпадают а 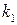 - различаются.
- различаются.
Для получения достоверных результатов принимают
 . (3.39)
. (3.39)
Следует заметить, что коэффициенты линеаризации зависят от закона распределения 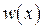 . Он обычно неизвестен. Как правило, при расчётах его полагают нормальным. Кроме того, коэффициенты
. Он обычно неизвестен. Как правило, при расчётах его полагают нормальным. Кроме того, коэффициенты 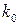 и
и 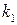 для типовых нелинейностей можно рассчитать предварительно.
для типовых нелинейностей можно рассчитать предварительно.
При расчётах статистически линеаризованной нелинейной системы исходная одноконтурная система заменяется эквивалентной двухконтурной (рис. 3.8) [4].
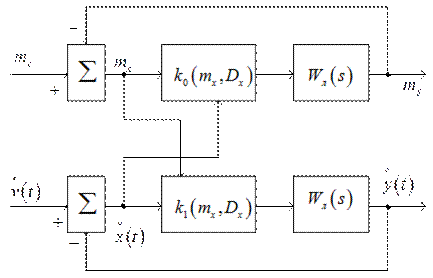
Рис. 3.8
Задающими воздействиями являются для верхнего канала - математическое ожидание 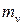 , а для нижнего центрированная случайная составляющая входного сигнала
, а для нижнего центрированная случайная составляющая входного сигнала  . Входной сигнал может быть линейной комбинацией полезного сигнала и помехи. Здесь
. Входной сигнал может быть линейной комбинацией полезного сигнала и помехи. Здесь 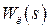 - передаточная функция линейной части системы.
- передаточная функция линейной части системы.
Для верхнего канала записывают уравнение по теореме о предельном значении функции:
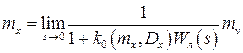 , (3.40)
, (3.40)
а для нижнего канала – уравнение для 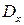 :
:
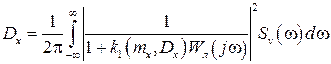 . (3.41)
. (3.41)
Решая систему (3.40) и (3.41), находят 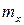 и
и 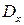 .
.
Конкретные примеры исследования статистически линеаризованных НСАУ рассматриваются в [4, 8].
Дата добавления: 2015-02-07; просмотров: 1411;
