Случайные процессы в импульсных системах

Будем рассматривать стационарные эргодические случайные дискретные (решётчатые) процессы 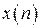как совокупность решётчатых реализаций . Здесь решётчатая реализация понимается как последовательность ординат, совпадающих с соответствующими значениями непрерывной реализации 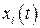в дискретные моменты времени 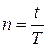, где 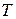- период квантования (дискретизации).

По аналогии с непрерывными системами вводятся статистические характеристики импульсных систем [4].

Среднее значение (математическое ожидание)

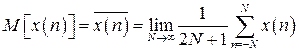, (3.24)

где 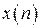- реализация дискретного процесса.

Дисперсия дискретного случайного процесса

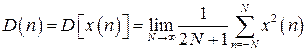. (3.25)

Корреляционная функция

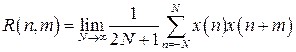, (3.26)

где 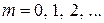− дискретные значения относительного времени.

При наличии двух случайных процессов вводят взаимную корреляционную функцию.

Спектральная плотность дискретного случайного процесса

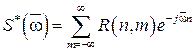, (3.27)

где 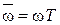− относительная частота.

Спектральная плотность 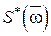дискретного случайного процесса связана со спектральной плотностью 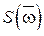соответствующего непрерывного случайного процесса формулой:

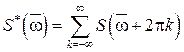. (3.28)

Спектральная плотность и корреляционная функция связаны с дисперсией:

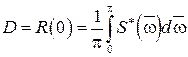. (3.29)

Расчёт импульсных систем при случайных воздействиях аналогичен расчёту непрерывных систем с учётом дискретных статистических характеристик. Чаще всего оценивают среднее значение квадрата дискретной ошибки. Если на вход импульсной системы поступают некоррелированные стационарные полезный сигнал 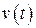и помеха 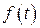, то спектральная плотность дискретной случайной ошибки

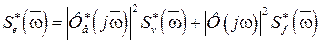, (3.30)

где 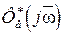и 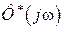- частотные передаточные замкнутой импульсной функции системы по ошибке и замкнутой системы, а 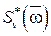и − дискретные спектральные плотности полезного сигнала и помехи.

Среднее значение квадрата дискретной ошибки

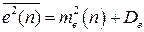, (3.31)

где 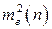- регулярная составляющая ошибки, а 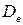- дисперсия ошибки.

Поскольку вычисления, связанные с оптимизационными задачами, громоздки, то эти исследования целесообразно проводить с помощью компьютерного моделирования.