Особенности синтеза систем автоматического управления

При синтезе систем со случайными воздействиями решается задача определения динамических характеристик системы, наилучшим образом обеспечивающих выполнение определённого статистического критерия оптимальности. Наиболее часто применяется критерий минимума среднеквадратичной ошибки системы. В простейшем случае, когда на систему воздействуют некоррелированные стационарные полезный сигнал 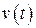и помеха 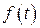, среднее значение квадрата ошибки .

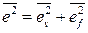Графики зависимости составляющих ошибки от коэффициента передачи разомкнутой системы (рис. 3.3) могут иметь вид, изображенный на рис. 3.5 .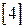

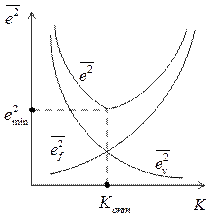
Рис. 3.5

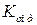Этот рисунок показывает, что ошибка системы по входному воздействию уменьшается с увеличением , но при этом расчёт ошибка от возмущения. Поэтому при одновременном воздействии на систему полезного сигнала и помехи необходимо находить оптимальное значение параметра, например , доставляющего ошибке минимальное значение .

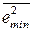При синтезе САУ возможны два вида задач: синтез при заданной структуре системы и синтез при произвольной структуре системы.

При решении первой задачи задаются структура системы, её передаточная функция, статистические характеристики полезного сигнала и помехи. Находятся оптимальные параметры регулятора (коэффициент передачи, постоянные времени), при которых обеспечивается минимум среднеквадратичной ошибки.

Задача решается так: находится средний квадрат ошибки 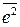, аналогично рассмотренному в подразделе 3.3; далее дифференцируют 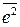по 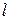интересующим параметрам и приравнивают нулю эти частные производные; решая систему из 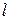уравнений, находят оптимальные значения этих параметров.

Для рассмотренного примера ; ; ; ; .

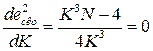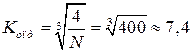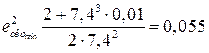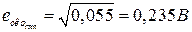В случае синтеза САУ при её произвольной структуре чаще всего рассматривают приложение воздействий к одной точке (рис. 3.6) .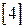

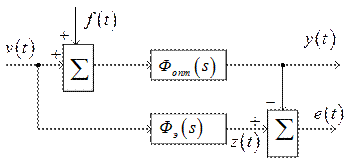
Рис. 3.6

На этой схеме 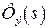- передаточная функция эталонной модели, 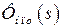- искомая передаточная функция замкнутой системы, обеспечивающая минимум среднему значению квадрата суммарной ошибки :

.

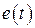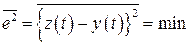При этом заданными считаются 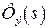, статистические характеристики полезного сигнала 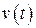и помехи .

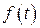Как показано в ,

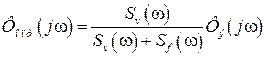, (3.20)

где 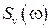и 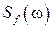- соответственно спектральные плотности полезного сигнала и помехи.

Однако частотную передаточную функцию (3.19) практически реализовать невозможно [4]. Для реализации функции, близкой к оптимальной, разлагают 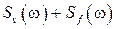на комплексные множители:

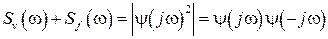, (3.21)

где 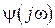- функция, все нули и полюсы которой лежат в верхней полуплоскости комплексной переменной , а 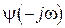- функция, комплексно-сопряжённая с 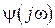, все нули и полюсы которой лежат в нижней полуплоскости переменной . Эту операцию называют “факторизацией”.

Далее осуществляют операцию “расщепления”, т.е. разделение 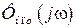на реализуемые и нереализуемые части:

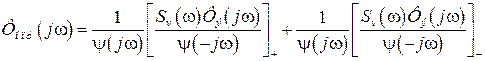, (3.22)

где реализуемая часть обозначена знаком “+”, а нереализуемая - знаком “−”. К нереализуемой части относят члены, содержащие звенья, у которых есть правые полюсы.

Нереализуемую часть отбрасывают. Близкая к оптимальной реализуемая частотная передаточная функция системы

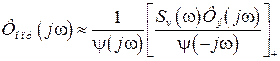. (3.23)

Заменяя в (3.23) на 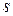, окончательно получают передаточную функцию замкнутой системы 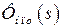, из которой можно получить передаточную функцию разомкнутой системы 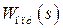и выбрать её элементы.