Вычисление коэффициентов гармонической линеаризации
Если нелинейная характеристика представлена в виде кусочно-линейной, то получить коэффициенты гармонической линеаризации несложно. Отметим общие свойства этих коэффициентов. Если 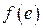 является нечетно-симметричной однозначной характеристикой, то всегда
является нечетно-симметричной однозначной характеристикой, то всегда 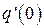 , а (2.46) будет иметь вид
, а (2.46) будет иметь вид
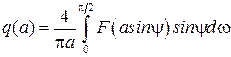 . (2.54)
. (2.54)
Для петлевых нечетно-симметричных характеристик можно в интегралах (2.46), (2.47) брать пределы интегрирования от 0 до 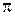 и удвоить полученные результаты.
и удвоить полученные результаты.
Рассмотрим простейший случай. Пусть 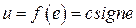 , т.е. рассматривается идеальное реле. Так как
, т.е. рассматривается идеальное реле. Так как 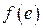 – однозначная нечетно-симметричная нелинейность, то
– однозначная нечетно-симметричная нелинейность, то 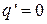 , а
, а
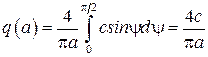 , (2.55)
, (2.55)
Для этой же характеристики для случая несимметричных колебаний можно получить
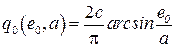 ,
, 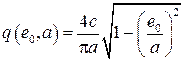 . (2.56)
. (2.56)
В литературе [6, 7] можно найти аналитические выражения коэффициентов гармонической линеаризации 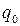 ,
, 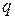 ,
, 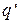 практически для любых видов нелинейностей, а также графики их зависимостей от величины амплитуды
практически для любых видов нелинейностей, а также графики их зависимостей от величины амплитуды 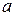 .
.
Дата добавления: 2015-02-07; просмотров: 1562;
