Метод точечного преобразования
Метод точечного преобразования является усовершенствованным методом припасовывания с привлечением геометрического аппарата фазовой плоскости и применяется в основном для анализа свободных режимов в системах второго порядка.
Пусть система описывается уравнениями (2.11), а уравнения для фазовых траекторий будут (2.13). На фазовой плоскости нарисуем отрезок линии 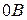 , как показано на рис. 2.12, который пересекается фазовыми траекториями в одном направлении. Пусть
, как показано на рис. 2.12, который пересекается фазовыми траекториями в одном направлении. Пусть 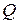 – начальная точка пересечения фазовой траекторией этого отрезка, а
– начальная точка пересечения фазовой траекторией этого отрезка, а 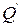 – последующая при движении по данной фазовой траектории. Обозначим через
– последующая при движении по данной фазовой траектории. Обозначим через 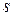 и
и 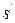 соответствующие расстояния точек
соответствующие расстояния точек 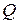 и
и 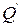 до точки 0 (начала координат). Точка
до точки 0 (начала координат). Точка 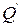 называется последующей по отношению к исходной (предыдущей) точке
называется последующей по отношению к исходной (предыдущей) точке 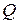 . Зависимость
. Зависимость
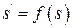 (2.36)
(2.36)
будем называть функцией последования, которая определяет закон точечного преобразования вдоль отрезка 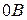 .
.
Так как фазовые траектории всюду плотно заполняют фазовое пространство, то исходные и последующие точки всюду плотно заполняют отрезок 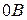 .
.
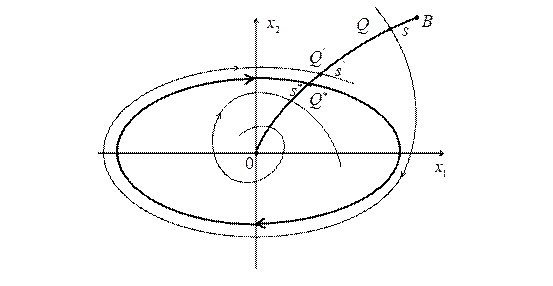
Рис. 2.12
По виду функции последования 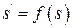 можно качественно судить о поведении фазовых траекторий и виде фазового портрета, а в ряде случаев и определить количественные характеристики процессов в системе.
можно качественно судить о поведении фазовых траекторий и виде фазового портрета, а в ряде случаев и определить количественные характеристики процессов в системе.
В соответствии, например, с рис. 2.12 можно сделать ряд следующих выводов. Если величина 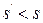 , то фазовые траектории приближаются к началу координат. Если
, то фазовые траектории приближаются к началу координат. Если 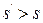 , то все фазовые траектории удаляются от начала координат. Если в процессе точечного преобразования
, то все фазовые траектории удаляются от начала координат. Если в процессе точечного преобразования 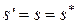 , то на фазовой плоскости существует замкнутая кривая, соответствующая предельному циклу.
, то на фазовой плоскости существует замкнутая кривая, соответствующая предельному циклу.
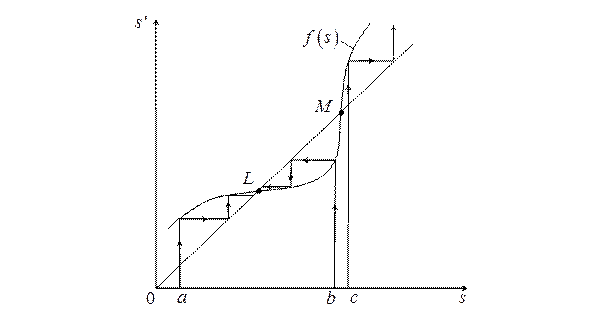
Рис. 2.13
Исследование поведения системы с помощью точечного преобразования удобно проводить, используя график функции 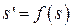 . На рис. 2.13 изображен график функции
. На рис. 2.13 изображен график функции 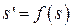 и через начало координат проведена прямая, совпадающая с биссектрисой первого квадранта плоскости
и через начало координат проведена прямая, совпадающая с биссектрисой первого квадранта плоскости 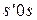 .
.
Ход точечного преобразования следующий. Выбираем исходную точку на оси 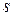 − точку
− точку 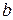 , для нее находим координату последующей точки на кривой
, для нее находим координату последующей точки на кривой 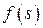 . Далее используем найденную последующую, принимаем ее за исходную и находим опять последующую. Ход точечного преобразования из точки
. Далее используем найденную последующую, принимаем ее за исходную и находим опять последующую. Ход точечного преобразования из точки 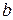 показан стрелками. Итак, по ходу стрелок видно, что мы приближаемся к точке
показан стрелками. Итак, по ходу стрелок видно, что мы приближаемся к точке 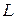 , в которой
, в которой 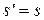 . Для исходной точки
. Для исходной точки 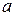 картина точечного преобразования повторяется. Таким образом, в точке
картина точечного преобразования повторяется. Таким образом, в точке 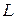 существует устойчивый предельный цикл (автоколебания). Обратная картина будет относительно точки
существует устойчивый предельный цикл (автоколебания). Обратная картина будет относительно точки 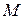 , где есть предельный цикл, но он неустойчив.
, где есть предельный цикл, но он неустойчив.
Графики, подобные приведенному на рис. 2.13, называются диаграммами точечного преобразования.
Определение функции 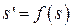 часто трудоемкая задача. Проще эту функцию задать в параметрической форме, когда
часто трудоемкая задача. Проще эту функцию задать в параметрической форме, когда 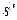 и
и 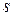 зависят от некоторого параметра. В качестве такого параметра выбирают величину
зависят от некоторого параметра. В качестве такого параметра выбирают величину 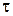 − время прохождения из точки
− время прохождения из точки 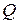 в последующую точку
в последующую точку 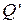 по ходу фазовой траектории. Итак, находят уравнения
по ходу фазовой траектории. Итак, находят уравнения
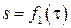 ,
, 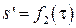 , (2.37)
, (2.37)
которые являются параметрической формой задания зависимости 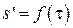 .
.
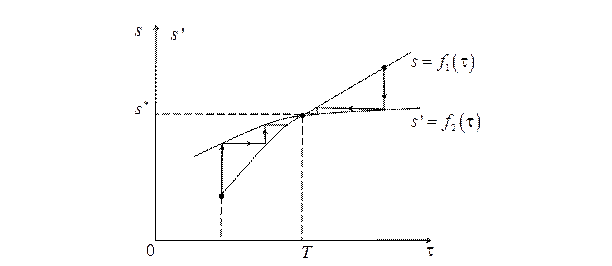
Рис. 2.14
На рис. 2.14 приведен пример точечного преобразования при параметрической форме задания кривых (2.37). Точка с координатами 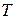 ,
, 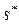 соответствует наличию устойчивого предельного цикла (автоколебаний). При этом величина
соответствует наличию устойчивого предельного цикла (автоколебаний). При этом величина 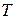 − период автоколебаний. Конкретные примеры применения точечного преобразования можно найти в [6, 7].
− период автоколебаний. Конкретные примеры применения точечного преобразования можно найти в [6, 7].
Дата добавления: 2015-02-07; просмотров: 2701;
