Скользящие режимы в нелинейных системах
Рассмотрим нелинейную САУ [7], изображенную на рис. 2.7, где  – модель идеального реле:
– модель идеального реле: 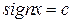 при
при 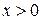 ,
, 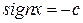 при
при 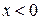 .
.
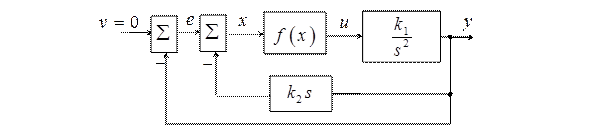
Рис. 2.7
В соответствии с рис. 2.7 уравнение системы будет
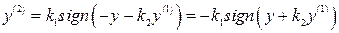 .
.
Вводя новые переменные  ,
, 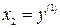 , получим систему уравнений
, получим систему уравнений
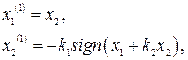
из которой находим уравнения для фазовых траекторий
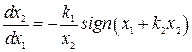 . (2.20)
. (2.20)
Уравнение линии переключения получим из условия  , т.е.
, т.е.
 . (2.21)
. (2.21)
В области фазовой плоскости при 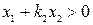 уравнение (2.20) имеет вид
уравнение (2.20) имеет вид
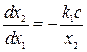 , (2.22)
, (2.22)
а там где 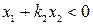 , уравнение (2.20) будет
, уравнение (2.20) будет
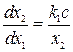 . (2.23)
. (2.23)
Решения уравнений (2.22), (2.23) соответственно имеют вид:
 , (2.24)
, (2.24)
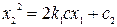 , (2.25)
, (2.25)
где 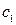 ,
, 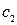 произвольные постоянные, которые определяются начальными условиями
произвольные постоянные, которые определяются начальными условиями 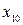 ,
, 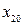 .
.
Уравнения (2.24), (2.25) на фазовой плоскости определяют параболы. Уравнение (2.24) справедливо справа от линии переключения (2.21), а (2.25) – слева.
На рис. 2.8 изображен фазовый портрет нелинейной системы, из которого следует, что на линии переключения существует отрезок АВ, на котором все фазовые траектории с двух сторон входят в этот отрезок. Изображающая точка, попав на этот отрезок, далее с течением времени обязана двигаться по нему к началу координат (положению равновесия). Такой режим называется скользящим режимом, а отрезок АВ отрезкомскольжения. На рис. 2.8 начальная точка 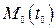 переходит по фазовым траекториям в точку
переходит по фазовым траекториям в точку 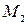 , затем в
, затем в  (попадает на отрезок скольжения) и далее по линии переключения обязана двигаться к началу координат, т.е. в системе возникает режим скольжения.
(попадает на отрезок скольжения) и далее по линии переключения обязана двигаться к началу координат, т.е. в системе возникает режим скольжения.
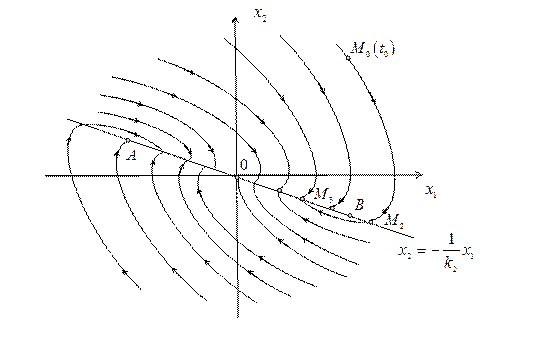
Рис. 2.8
Найдем координаты точек А, В, т.е. длину отрезка скольжения. В точке А касательная к параболе должна совпадать с линией переключения, т.е. 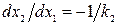 . Тогда с учетом (2.22) будем иметь
. Тогда с учетом (2.22) будем иметь 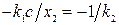 , т.е. ордината точки А будет
, т.е. ордината точки А будет 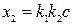 .
.
Аналогично, ордината точки В будет 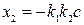 . Таким образом, длина отрезка АВ будет тем больше, чем больше
. Таким образом, длина отрезка АВ будет тем больше, чем больше 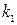 или
или 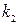 .
.
Найдем закон движения в скользящем режиме. На линии переключения (2.21)  , но
, но 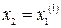 , откуда имеет место следующее уравнение
, откуда имеет место следующее уравнение
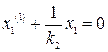 , (2.26)
, (2.26)
определяющее закон движения в скользящем режиме. Решение уравнения (2.26) имеет вид 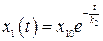 .
.
Таким образом, на линии скольжения исходная нелинейная система второго порядка вырождается в линейную систему первого порядка (2.26), причем параметры процесса скольжения не зависят от параметров прямой цепи 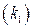 . Меняя
. Меняя 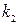 , можно менять время попадания изображающей точки в начало координат, т.е. фактически время регулирования. Чем меньше величина
, можно менять время попадания изображающей точки в начало координат, т.е. фактически время регулирования. Чем меньше величина 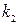 , тем меньше время регулирования.
, тем меньше время регулирования.
Дата добавления: 2015-02-07; просмотров: 3087;
