Построение фазовых траекторий
Аналитическое выражение для фазовой траектории является решением нелинейных дифференциальных уравнений (2.13), (2.14) и найти его в общем случае невозможно. Однако если представить реальные нелинейные характеристики в виде идеальных, т.е. аппроксимированных на отдельных участках прямыми линиями, то возможно применение аналитических методов решения. Суть такого подхода заключается в следующем. Пусть идеальная нелинейность на некотором интервале 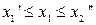 описывается линейной характеристикой
описывается линейной характеристикой 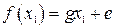 , где
, где 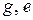 – заданные коэффициенты. В этом случае уравнение (2.13) для фазовых траекторий будет иметь вид
– заданные коэффициенты. В этом случае уравнение (2.13) для фазовых траекторий будет иметь вид
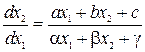 , (2.18)
, (2.18)
где 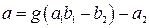 ,
, 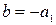 ,
, 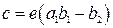 ,
, 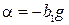 ,
, 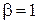 ,
, 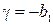 .
.
Уравнение (2.18) является частным случаем уравнения Якоби и может быть проинтегрировано, т.е. задавая начальные значения 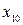 ,
, 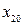 можно найти вид фазовой траектории
можно найти вид фазовой траектории 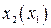 при условии, что
при условии, что 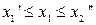 .
.
Таким образом, разбивая всю ось 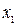 на ряд интервалов
на ряд интервалов 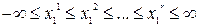 и аппроксимируя нелинейность
и аппроксимируя нелинейность 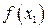 линейной зависимостью
линейной зависимостью 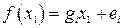 на каждом интервале, получим свое уравнение (2.18), решение которого даст на этом интервале некоторою фазовую траекторию. Линии, соответствующие равенствам
на каждом интервале, получим свое уравнение (2.18), решение которого даст на этом интервале некоторою фазовую траекторию. Линии, соответствующие равенствам 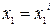 на плоскости
на плоскости 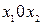 , разделят ее на ряд областей. Эти линии, границы областей, будем называть линиями переключения.
, разделят ее на ряд областей. Эти линии, границы областей, будем называть линиями переключения.
При попадании изображающей точки фазовой траектории на линию переключения, конечное значение этой фазовой траектории, т.е. значения координат 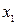 и
и 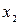 на ее конце, принимаются за начальные условия для фазовой траектории в смежной области. Такой метод решения дифференциального уравнения называют методом сшивания, склеивания или припасовывания решений.
на ее конце, принимаются за начальные условия для фазовой траектории в смежной области. Такой метод решения дифференциального уравнения называют методом сшивания, склеивания или припасовывания решений.
Другой способ построения фазовых траекторий – это метод изоклин, который является графическим методом. В уравнении для фазовых траекторий (2.13) правая часть в каждой точке фазовой плоскости с координатами 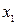 ,
, 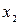 определяет скорость движения изображающей точки, т.е. определяет угол наклона касательной к фазовой траектории в этой точке. Уравнение
определяет скорость движения изображающей точки, т.е. определяет угол наклона касательной к фазовой траектории в этой точке. Уравнение
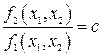 , (2.19)
, (2.19)
где 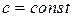 произвольное число, определяет линию на фазовой плоскости равных значений производных или углов наклона касательной. Эту линию и называют изоклиной.
произвольное число, определяет линию на фазовой плоскости равных значений производных или углов наклона касательной. Эту линию и называют изоклиной.
Изобразив на фазовой плоскости несколько изоклин с соответствующими направлениями касательных, можно приближенно представить вид фазовых траекторий и вид фазового портрета.
Наконец, возможно построение фазового портрета путем моделирования уравнений фазовых траекторий и их решения на компьютере.
Дата добавления: 2015-02-07; просмотров: 1996;
