Классификация фазовых портретов

В первую очередь выделяются точки равновесного состояния системы, в которых в (2.11) 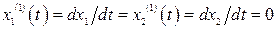и которые определяются из решения системы нелинейных уравнений

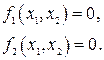(2.15)

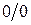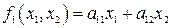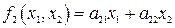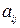В этих точках правая часть уравнения (2.13) является неопределенностью вида . Поэтому точки равновесного состояния еще называют особыми точками на фазовой плоскости. Особые точки классифицируются по их типу для линейных систем. В линейном случае в (2.10) , , где – постоянные коэффициенты, и особая точка будет единственной 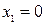, , 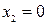т.е. начало координат на фазовой плоскости. Тип особой точки определяют корнями характеристического уравнения линейной системы

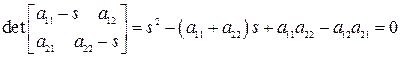. (2.16)

Различают восемь типов особых точек:

1. устойчивый узел – два различных действительных отрицательных корня;

2. вырожденный устойчивый узел – два равных действительных отрицательных корня;

3. устойчивый фокус – два комплексно-сопряженных корня с отрицательными действительными частями;

4. центр – два чисто мнимых корня;

5. неустойчивы узел – два различных действительных положительных корня;

6. вырожденный неустойчивый узел – два равных действительных положительных корня;

7. неустойчивый фокус – два комплексно-сопряженных корня с положительными действительными частями;

8. седло – два различных действительных корня с разными знаками.

Фазовые портреты линейных систем с соответствующим типом особой точки приводятся в [4, 6, 7]. Например, для точки типа центр фазовые траектории – это симметричные эллипсы на плоскости 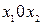, охватывающие начало координат. Для точек типа устойчивый и неустойчивый фокус – это логарифмические спирали, соответственно скручивающиеся к началу координат и раскручивающиеся.

Отметим, что первые три типа точек соответствуют устойчивой линейной системе, четвертый тип – нейтральной или находящейся на границе устойчивости системе, а все точки, начиная с четвертого типа и далее, относятся к неустойчивой линейной системе.

Классификацию особых точек нелинейных систем производят по линеаризованной модели нелинейной системы вблизи исследуемой особой точки. Из уравнений (2.15) после их решения находим координаты особой точки 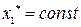, 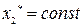(таких точек может быть несколько и даже бесчисленное множество).

Исходное уравнение (2.11) подвергаем линеаризации относительно найденных координат , 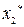путем разложения функций 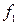, 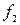в ряд Тейлора [1]. В результате будем иметь уравнения первого приближения

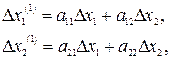
где 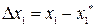, , 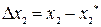а коэффициенты 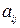определяются следующим образом

. (2.17)

Подставляем найденные 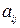в (2.16), определяем вид корней уравнения (2.16) и тип особой точки нелинейной системы. Если особых точек несколько, процедуру проделываем для каждой особой точки.

Кроме особых точек фазовые портреты нелинейных систем могут иметь еще особые кривые (траектории), что не характерно для линейных систем. Из особых кривых выделим в первую очередь два типа: сепаратрисы и предельные циклы. Сепаратриса – это особая кривая, которая разделяет на фазовой плоскости области с разными типами фазовых траекторий. Предельные циклы – это замкнутые кривые, соответствующие периодическим процессам.

Предельный цикл называется устойчивым предельным циклом, если все фазовые траектории, начинающиеся внутри и за пределами предельного цикла с течением времени стремятся к нему (навиваются на него изнутри и снаружи). Если фазовые траектории снаружи либо изнутри с течением времени удаляются от него, то будем иметь неустойчивый предельный цикл.

Устойчивый предельный цикл (устойчивый периодический процесс) физически соответствует возникновению в системе автоколебаний, которые могут возникать при отсутствии внешнего воздействия, причем их амплитуда и частота не зависит от начальных условий, а определяются внутренними свойствами.

Например, в линейной системе возможен периодический (гармонический) режим рис. 2.3, 2.4 (кривые 1), однако он не является автоколебанием, т.к. его амплитуда зависит от начальных условий.

На рис. 2.5 представлены примеры фазовых портретов нелинейной системы, где жирными линиями выделены предельные циклы. На рис. 2.5 а предельный цикл является устойчивым (автоколебание), а положение равновесия (начало координат) неустойчиво. Вариант рис. 2.5 б дает неустойчивый предельный цикл, а положение равновесия устойчиво. Наконец, в варианте рис. 2.5 в внешний предельный цикл устойчивый (автоколебание), внутренний неустойчив, а положение равновесия устойчиво.

Рис. 2.5

Пример 2.2. Рассмотрим нелинейную систему [7], описываемую уравнениями

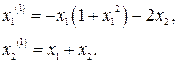
Уравнения фазовых траекторий будут

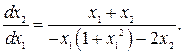
Особые точки найдем из решения системы уравнений

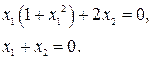
Это особые точки с координатами (0, 0), (1, -1), (-1, 1).

Исследуем первую особую точку (начало координат) 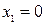, , 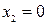для которой нетрудно найти (2.17) 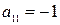, , 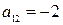, , 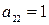а уравнение (2.16) соответственно будет .

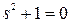Корни этого уравнения будут чисто мнимые 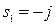, 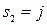. В соответствии с классификацией особая точка – начало координат будет типа центр. Аналогично, можно показать, что две другие особые точки (1,-1), (-1,1) будут типа седло. На рис. 2.6 дан общий фазовый портрет системы, где жирным выделены кривые, которые являются сепаратрисами.

Рис. 2.6