Система с переменной структурой
Структура нелинейной САУ изображена на рис. 2.9.

Рис. 2.9
На этом рисунке нелинейным элементом является логическое устройство, которое на основе измерения сигнала 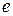 управляет по определенному закону ключом
управляет по определенному закону ключом 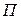 , так что передаточная функция разомкнутой системы может быть либо
, так что передаточная функция разомкнутой системы может быть либо 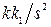 , либо
, либо 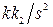 , т.е. система в процессе работы меняет свою структуру. При включении верхнего звена уравнение замкнутой системы имеет вид
, т.е. система в процессе работы меняет свою структуру. При включении верхнего звена уравнение замкнутой системы имеет вид
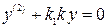 , (2.27)
, (2.27)
а при включении нижнего звена
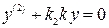 . (2.28)
. (2.28)
Характеристическое уравнение такой замкнутой системы будет 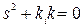 и, если
и, если 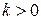 ,
, 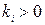 , имеет два комплексных корня, т.е. система является нейтральной или находиться на границе устойчивости. Такая система является неработоспособной.
, имеет два комплексных корня, т.е. система является нейтральной или находиться на границе устойчивости. Такая система является неработоспособной.
Обозначим 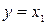 ,
, 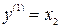 , тогда уравнения для фазовых траекторий будут
, тогда уравнения для фазовых траекторий будут
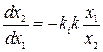 ,
, 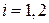 . (2.29)
. (2.29)
Решая уравнения (2.29), получим на фазовой плоскости семейство эллипсов
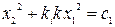 ,
,
где 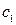 – произвольная постоянная.
– произвольная постоянная.
Путем подбора 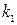 ,
, 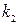 сделаем одни эллипсы сжатыми вдоль оси
сделаем одни эллипсы сжатыми вдоль оси 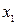 , а другие вдоль оси
, а другие вдоль оси 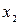 , как это изображено на рис. 2.10.
, как это изображено на рис. 2.10.
Закон переключения ключа выберем следующий: если 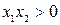 , то имеем цепь с коэффициентом
, то имеем цепь с коэффициентом 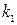 (рис. 2.10, а), если
(рис. 2.10, а), если 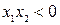 , то имеем цепь с коэффициентом
, то имеем цепь с коэффициентом 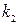 (рис. 2.10, б). Линиями переключения будут координатные оси фазовой плоскости
(рис. 2.10, б). Линиями переключения будут координатные оси фазовой плоскости 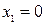 ,
, 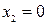 . Итак, если изображающая точка находится, например, в первом квадранте, то с течением времени она движется вниз вдоль эллипса до линии переключения
. Итак, если изображающая точка находится, например, в первом квадранте, то с течением времени она движется вниз вдоль эллипса до линии переключения 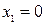 (рис. 2.10, а) и далее при
(рис. 2.10, а) и далее при 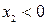 вдоль эллипса, сжатого относительно оси
вдоль эллипса, сжатого относительно оси 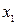 и т.д. Таким образом, с течением времени изображающая точка будет стремиться к началу координат.
и т.д. Таким образом, с течением времени изображающая точка будет стремиться к началу координат.
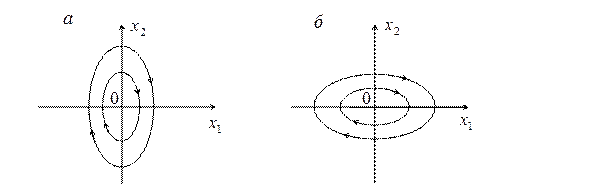
Рис. 2.10
В рассмотренном случае процесс будет колебательным. Однако возможно в такой системе организовать скользящий режим. Пусть в структуре рис. 2.9 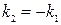 , тогда уравнения для фазовых траекторий будут
, тогда уравнения для фазовых траекторий будут
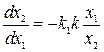 ,
, 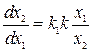 ,
,
первое из которых при  ,
, 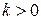 описывает эллипсы, а второе при
описывает эллипсы, а второе при  ,
, 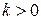 гиперболы на фазовой плоскости. Первый контур соответствует, как и раньше, нейтральной системе, а второй – неустойчивой системе. Переключение организуем следующим образом: если
гиперболы на фазовой плоскости. Первый контур соответствует, как и раньше, нейтральной системе, а второй – неустойчивой системе. Переключение организуем следующим образом: если 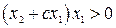 , работает верхняя цепь (коэффициент
, работает верхняя цепь (коэффициент 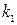 ), а если
), а если 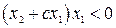 , работает нижняя цепь (коэффициент
, работает нижняя цепь (коэффициент 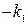 ). Таким образом, линиями переключения будут
). Таким образом, линиями переключения будут 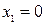 (ось ординат) и прямая
(ось ординат) и прямая 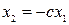 , где
, где 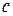 – параметр, который можно выбирать. Линия скольжения в данном случае не ограничена конечным отрезком, а является всей прямой
– параметр, который можно выбирать. Линия скольжения в данном случае не ограничена конечным отрезком, а является всей прямой 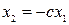 . Фазовый портрет изображен на рис. 2.11, где волнистая линия – это линия переключения.
. Фазовый портрет изображен на рис. 2.11, где волнистая линия – это линия переключения.

Рис. 2.11
Дата добавления: 2015-02-07; просмотров: 1752;
