Преобразование уравнений состояния
Пусть система описывается уравнениями состояния общего вида (8.3). Сделаем в этих уравнениях замену переменных x = Qz, где 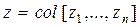 – новый вектор состояния, Q – произвольная матрица размерностью
– новый вектор состояния, Q – произвольная матрица размерностью 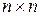 с постоянными коэффициентами. На матрицу Q накладывается единственное ограничение – она должна быть невырожденной (неособенной), т.е. определитель этой матрицы
с постоянными коэффициентами. На матрицу Q накладывается единственное ограничение – она должна быть невырожденной (неособенной), т.е. определитель этой матрицы 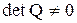 . В этом случае всегда существует обратная матрица, которую будем обозначать через
. В этом случае всегда существует обратная матрица, которую будем обозначать через 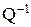 , такая, что
, такая, что 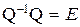 , где
, где 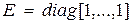 – единичная матрица размерностью
– единичная матрица размерностью 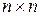 . Очевидно, что при этих условиях существует однозначная связь между векторами x и z:
. Очевидно, что при этих условиях существует однозначная связь между векторами x и z: 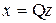 ,
, 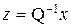 .
.
В уравнениях (8.3) сделаем замену x = Qz и с учетом того, что 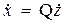 , получим
, получим
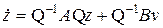 ,
, 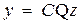 . (8.8)
. (8.8)
Уравнения (8.8) будут новыми уравнениями состояния, имеющими основную матрицу системы 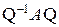 , входа
, входа 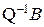 и выхода CQ. Так как Q – произвольная матрица, то исходным уравнениям (8.3) соответствует бесчисленное количество эквивалентных уравнений состояния (8.8).
и выхода CQ. Так как Q – произвольная матрица, то исходным уравнениям (8.3) соответствует бесчисленное количество эквивалентных уравнений состояния (8.8).
Отметим, что две матрицы A и 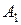 , связанные преобразованием
, связанные преобразованием 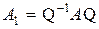 , называются подобными. Подобные матрицы имеют одинаковые собственные значения.
, называются подобными. Подобные матрицы имеют одинаковые собственные значения.
Используя линейное преобразование, можно поставить задачу о выборе при исследовании той или иной формы уравнений состояния. Наиболее часто решается задача преобразования исходной системы (8.3) к нормальной или канонической форме уравнений состояния (8.8).
Доказано, что для произвольной матрицы А всегда существует невырожденная квадратная матрица размерностью 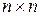 , которую обозначим через M и назовем модальной, такая, что матрица
, которую обозначим через M и назовем модальной, такая, что матрица 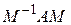 будет иметь форму Жордана. Если матрица А имеет различные собственные значения (числа)
будет иметь форму Жордана. Если матрица А имеет различные собственные значения (числа) 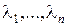 , являющиеся корнями характеристического уравнения
, являющиеся корнями характеристического уравнения
 , (8.9)
, (8.9)
то матрица 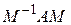 будет диагональной:
будет диагональной: 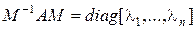 .
.
Таким образом, преобразование произвольной системы уравнений (8.3) к канонической форме всегда возможно. Наиболее просто задача определения модальной матрицы решается для случая различных собственных чисел матрицы А, которые обозначим через 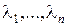 . Для каждого собственного числа
. Для каждого собственного числа 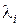 находится собственный вектор
находится собственный вектор  из решения векторно-матричного уравнения
из решения векторно-матричного уравнения
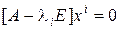 . (8.10)
. (8.10)
Матрица, образованная вектор-столбцами 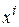 , т.е. матрица
, т.е. матрица
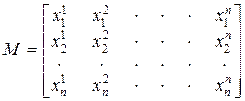 , (8.11)
, (8.11)
и будет искомой модальной матрицей.
В соответствии с (8.9) при 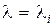 определитель системы линейных уравнений (8.10) равен нулю, т.е. система имеет бесчисленное множество решений, каждое из которых можно принять за собственный вектор. Отсюда матрица М является неединственной.
определитель системы линейных уравнений (8.10) равен нулю, т.е. система имеет бесчисленное множество решений, каждое из которых можно принять за собственный вектор. Отсюда матрица М является неединственной.
В случае кратных собственных значений матрицы А задача определения модальной матрица значительно усложняется.
В частности, если исходная матрица А является матрицей Фробениуса
вида
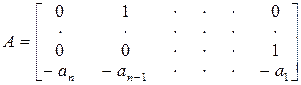 (8.12)
(8.12)
и собственные числа 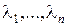 , являющиеся корнями характеристического уравнения
, являющиеся корнями характеристического уравнения
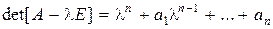 = 0, (8.13)
= 0, (8.13)
различны, то модальная матрица будет иметь вид
 . (8.14)
. (8.14)
Пример 8.3. Пусть в САУ, которая рассматривалась в примерах 8.1 и 8.2, 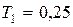 с,
с, 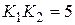 , тогда уравнения (8.7) будут иметь вид
, тогда уравнения (8.7) будут иметь вид
 ,
, 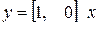 . (8.15)
. (8.15)
Преобразуем уравнения состояния к канонической форме. Основная матрица системы А является матрицей Фробениуса. Найдем ее собственные значения из решения характеристического уравнения
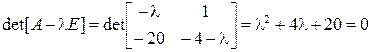 .
.
Корни уравнения будут различными: 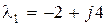 ,
, 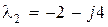 . Таким образом, в соответствии с (8.14) определяем модальную матрицу M и обратную ей
. Таким образом, в соответствии с (8.14) определяем модальную матрицу M и обратную ей 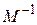 :
:
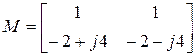 ,
, 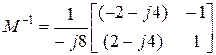 .
.
Далее M–1AM = diag[–2+ j4, –2 – j4],  ,
, 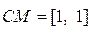 .
.
Итак, уравнения состояния (8.15) преобразуются к канонической форме:
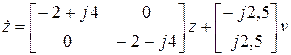 ,
, 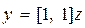 .
.
Пример 8.4. Пусть система описывается уравнениями состояния
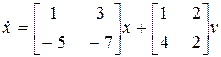 ,
, 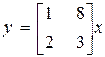 .
.
Корни характеристического уравнения 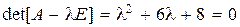 будут
будут 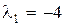 ,
,  .
.
Находим собственные векторы из решения системы линейных уравнений 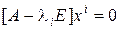 ,
,  .
.
Полагая 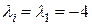 , будем иметь
, будем иметь
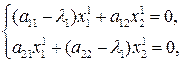
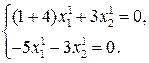
Из последних двух уравнений 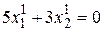 , откуда, задавая, например,
, откуда, задавая, например, 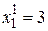 , получим
, получим 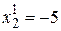 . Итак, первый собственный вектор
. Итак, первый собственный вектор 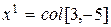 . При
. При 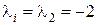 в конечном итоге для определения координат второго собственного вектора получим
в конечном итоге для определения координат второго собственного вектора получим 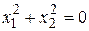 . Полагая
. Полагая 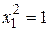 , будем иметь
, будем иметь 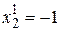 и соответственно
и соответственно  . Итак, матрицу М можно выбрать в виде
. Итак, матрицу М можно выбрать в виде
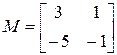 ,
, 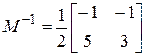 .
.
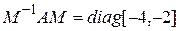 ,
, 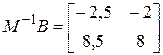 ,
, 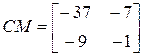 .
.
Окончательно уравнения в канонической форме будут иметь следующий вид:
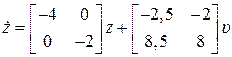 ,
, 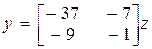 .
.
Дата добавления: 2015-02-07; просмотров: 926;
