Схемы моделирования и виды уравнений состояния

В зависимости от структуры матрицы А в (8.3) из общего класса уравнений состояния выделяют два подкласса. Если матрица А в (8.3) является диагональной:

(8.5)

или в общем случае представлена в форме Жордана, то имеем каноническую форму уравнений состояния. Примером матрицы в форме Жордана может служить матрица

размерностью 4×4, имеющая одну клетку Жордана размерностью 3×3.

Если матрица А в (8.3) представлена в виде

, (8.6)

то уравнения состояния имеют нормальную форму. Матрицу такой структуры называют сопровождающей матрицей или матрицей Фробениуса.

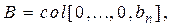
Пусть в уравнении (8.3) матрица , т.е. , 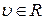и матрица А является матрицей Фробениуса (8.6). Тогда, очевидно, 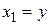, ,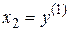…, , 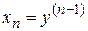т.е. в качестве переменных состояния выбрана сама выходная координата y и ее производные. В этом частном случае вектор состояния называют фазовым вектором, а пространство состояния – фазовым пространством.

Для более ясного понимания внутренней структуры и взаимосвязи отдельных переменных системы, описываемой уравнениями состояния, применяют графическую интерпретацию уравнений состояния в виде структурных схем, которые иногда называют схемами моделирования. При этом используются три основных блока, показанные на рис. 8.1: а) сумматор ,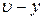
б) интегратор , в) блок преобразования (усиления) , где
А – некоторая матрица.

Рис. 8.1

Используя указанные блоки, можно изобразить схему моделирования по уравнениям (8.2), представленную на рис. 8.2.

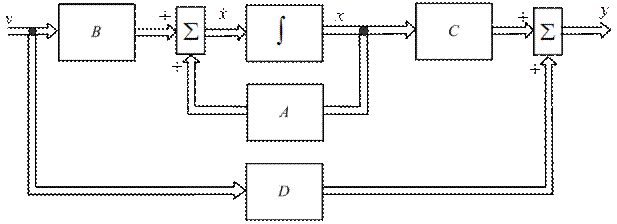
Рис. 8.2

Пример 8.2. Рассмотрим САУ из примера 8.1. В соответствии с полученными уравнениями состояния (8.4) нетрудно изобразить схему моделирования, представленную на рис. 8.3.

Рис. 8.3

Для этого же примера получим другую структуру схемы моделирования и соответственно другую форму уравнений состояния. Выходной сигнал y и сигнал ошибки e можно связать следующим уравнением в области изображений: 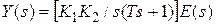, откуда нетрудно получить дифференциальное уравнение разомкнутой системы 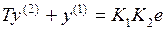. С учетом уравнения замыкания 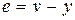получим дифференциальное уравнение замкнутой системы 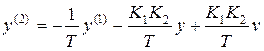, в соответствии с которым нетрудно получить схему моделирования (рис. 8.4).

Если обозначить выходы интеграторов через 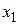и 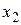, как показано на рис. 8.4, то можно в соответствии со схемой моделирования записать следующие уравнения: , , .

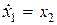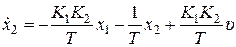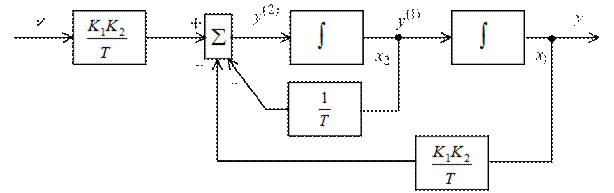
Рис. 8.4

Вводя вектор состояния , уравнения представим в виде

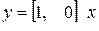, . (8.7)

Уравнения (8.4) и (8.7) имеют различный вид, как и схемы моделирования (см. рис. 8.3 и 8.4), но описывают одну и ту же систему. Уравнения состояния (8.7) имеют нормальную форму, они составлены относительно фазовых координат.