Описание систем управления с помощью уравнений состояния
Рассматриваемые в предыдущих разделах системы относятся к простейшему (классическому) типу САУ, характеризуемому одной регулируемой координатой (одномерные системы). Динамические процессы в них удобно описывать одним дифференциальным уравнением n-го порядка, передаточными функциями и частотными характеристиками. При описании многомерных или многосвязных систем, имеющих несколько регулируемых координат, такой подход встречает определенные трудности. Более естественной формой математического описания многомерных систем является векторно-матричная форма уравнений динамики или подход, базирующийся на применении уравнений состояния.
Преимуществом математических моделей в виде уравнений состояния является универсальность (применимость как для одномерных, так и для многомерных систем), компактность формы записи, а также более естественная форма записи для численных расчетов на ЭВМ. В силу этого с конца 60-х годов ХХ столетия в теории управления развиваются методы описания и исследования САУ на базе уравнений состояния.
При математическом описании любой системы всегда можно выделить три группы величин: 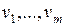 – входные сигналы, действующие на систему, включающие как управляющие, так и возмущающие сигналы;
– входные сигналы, действующие на систему, включающие как управляющие, так и возмущающие сигналы; 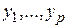 – выходные сигналы, несущие информацию о поведении системы, а также переменные
– выходные сигналы, несущие информацию о поведении системы, а также переменные 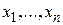 , характеризующие непосредственно саму систему (переменные состояния). физический смысл переменных
, характеризующие непосредственно саму систему (переменные состояния). физический смысл переменных 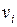 и
и 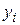 достаточно ясен. Переменные состояния
достаточно ясен. Переменные состояния 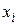 – это минимальный набор физических или абстрактных величин, который полностью определяет состояние системы в любой момент времени.
– это минимальный набор физических или абстрактных величин, который полностью определяет состояние системы в любой момент времени.
Объединим соответствующие группы переменных в векторы: 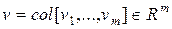 – вектор входа системы,
– вектор входа системы, 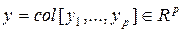 – вектор выхода системы (вектор наблюдения),
– вектор выхода системы (вектор наблюдения), 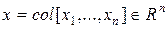 – вектор состояния,
– вектор состояния, 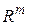 ,
, 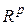 ,
, 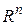 – евклидовы пространства соответствующих размерностей. Пространство
– евклидовы пространства соответствующих размерностей. Пространство 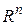 носит название пространства состояний.
носит название пространства состояний.
Так как нас интересует поведение системы во времени, т.е. динамика системы, то все соответствующие переменные и векторы будем полагать в дальнейшем функциями текущего времени t, т.е. 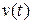 ,
, 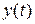 ,
, 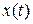 .
.
Под математической моделью системы будем понимать соотношения между векторами 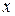 ,
, 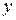 ,
, 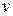 , описываемые при помощи математических операций и позволяющие однозначно определять закон изменения во времени
, описываемые при помощи математических операций и позволяющие однозначно определять закон изменения во времени
вектора выхода 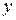 при заданном векторе входа
при заданном векторе входа 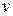 и начальном состоянии
и начальном состоянии
системы x.
В случае непрерывных систем наиболее общей формой математической модели являются уравнения вида

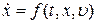 ,
, 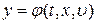 , (8.1)
, (8.1)
где 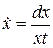 ,
, 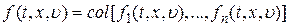 ,
, 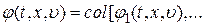
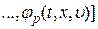 – вектор-функции соответствующих размерностей;
– вектор-функции соответствующих размерностей; 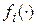 ,
, 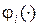 – скалярные функции.
– скалярные функции.
Уравнения (8.1) носят названия уравнений состояния, первое из которых будем называть уравнением входа, а второе – уравнением выхода.
Уравнения (8.1) описывают динамику нелинейной нестационарной непрерывной системы с сосредоточенными параметрами. Если 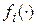 ,
, 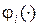 в явном виде не зависят от времени t, то имеем соответствующую модель стационарной системы.
в явном виде не зависят от времени t, то имеем соответствующую модель стационарной системы.
Если в некоторой области изменения переменных функции 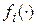 ,
, 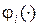 являются линейными, то уравнения (8.1) превращаются в линейные уравнения состояния
являются линейными, то уравнения (8.1) превращаются в линейные уравнения состояния
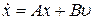 ,
, 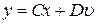 , (8.2)
, (8.2)
где А, В, C, D – соответственно матрицы размерностей 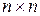 ,
, 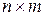 ,
, 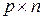 ,
, 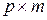 .
.
Если коэффициенты всех матриц не зависят в явном виде от времени,
то имеем модель линейной стационарной системы. Если хотя бы один из
коэффициентов этих матриц в явном виде зависит от t, то модель будет
нестационарной.
Для физически реализуемых систем всегда D = 0 (здесь и далее равенство матрицы нулю подразумевает равенство нулевой матрице) и чаще всего рассматриваются уравнения состояния вида
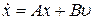 ,
, 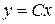 . (8.3)
. (8.3)
Матрица А называется основной матрицей системы, В – матрицей входа,
С – матрицей выхода, D – матрицей связи.
В данном разделе будем рассматривать только линейные стационарные системы, описываемые уравнениями (8.2), (8.3).
Отметим ряд дополнительных моментов, касающихся приведенных моделей систем:
1. Для полного описания поведения системы всегда требуется задать ее начальное состояние в некоторый момент времени (чаще всего нулевой). Это соответствует заданию начальных условий для дифференциальных уравнений, входящих в (8.1)–(8.3). Итак, в (8.1)–(8.3) всегда подразумевается задание x(0).Чаще всего 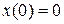 .
.
2. Элементы матриц А, В, С, D и векторов 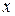 ,
, 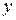 ,
, 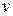 в общем случае могут быть комплексными величинами.
в общем случае могут быть комплексными величинами.
3. В (8.1)–(8.3) величины 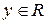 ,
, 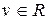 могут быть скалярными, т.е. уравнения (8.1)–(8.3) могут описывать как многомерные, так и одномерные системы.
могут быть скалярными, т.е. уравнения (8.1)–(8.3) могут описывать как многомерные, так и одномерные системы.
4. Уравнениями (8.1)–(8.3) могут быть описаны любые динамические системы: отдельные элементы и устройства, объект управления, регулятор, вся САУ в целом.
Пример 8.1. Рассмотрим САУ стандартной структуры, изображенной на рис. 3.1. Пусть 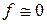 ,
, 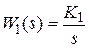 ,
, 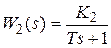 , а выход звена
, а выход звена 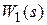 (соответственно вход
(соответственно вход 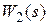 ) обозначим через u.
) обозначим через u.
При этом несложно получить следующие уравнения: 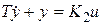 ,
, 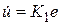 ,
, 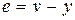 , а после введения новых переменных
, а после введения новых переменных 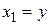 ,
, 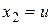 – уравнения состояния
– уравнения состояния
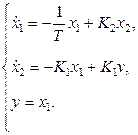
Векторно-матричная модель системы будет иметь вид
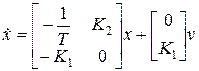 ,
, 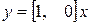 . (8.4)
. (8.4)
Дата добавления: 2015-02-07; просмотров: 1180;
