Каноническая форма уравнений состояния одномерной системы
Для получения уравнений состояния одномерной системы в канонической форме используется передаточная функция системы. Будем полагать, что система описывается дифференциальным уравнением (8.16), которому соответствует передаточная функция 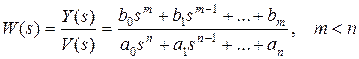 .
.
Пусть характеристическое уравнение системы имеет n различных корней 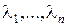 , тогда передаточную функцию можно представить в виде
, тогда передаточную функцию можно представить в виде
 . (8.22)
. (8.22)
Очевидно, что в этом случае  .
.
Обозначим 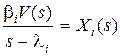 , тогда
, тогда 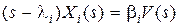 ,
, 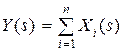 .
.
Перейдем в операторных соотношениях к оригиналам, полагая 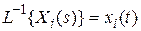 . Получим
. Получим 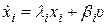 ,
, 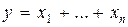 ,
, 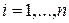 .
.
Вводя вектор состояния 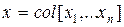 , запишем полученные уравнения в виде уравнений состояния
, запишем полученные уравнения в виде уравнений состояния
 . (8.23)
. (8.23)
Итак, получили уравнения состояния в канонической форме с диагональной матрицей коэффициентов, где в общем случае элементы 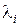 ,
,  матриц могут быть и комплексными величинами.
матриц могут быть и комплексными величинами.
Из (8.22) можно получить другую каноническую форму уравнений состояния. Если обозначить  , то проводя аналогичные рассуждения, получим уравнения состояния:
, то проводя аналогичные рассуждения, получим уравнения состояния:
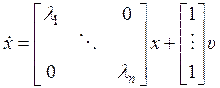 ,
, 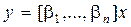 . (8.24)
. (8.24)
Рассмотрим теперь случай кратных корней. Пусть характеристическое уравнение имеет корни 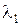 кратности k, а остальные корни
кратности k, а остальные корни 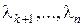 простые.
простые.
Тогда передаточную функцию можно представить в виде разложения
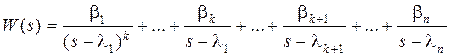 ,
,
где 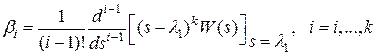 ,
,
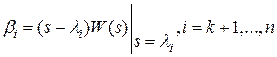 .
.
в этом случае 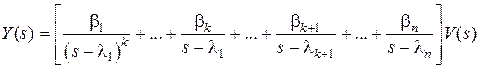 или
или 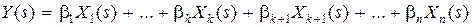 .
.
Между изображениями 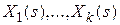 существует связь
существует связь 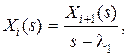
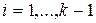 . Полагая
. Полагая 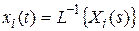 и переходя к оригиналам, получим в области оригиналов:
и переходя к оригиналам, получим в области оригиналов: 
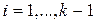 ;
; 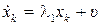 ;
; 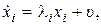
 ;
; 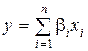 .
.
Вводя вектор состояния 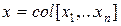 , полученные соотношения запишем в векторно-матричной форме:
, полученные соотношения запишем в векторно-матричной форме:
|

Уравнения состояния (8.25) имеют каноническую форму, основная матрица – форму Жордана. Корню кратности k соответствует клетка Жордана размерностью 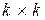 . Очевидно, при наличии нескольких кратных корней будем получать соответствующие клетки Жордана для каждого корня.
. Очевидно, при наличии нескольких кратных корней будем получать соответствующие клетки Жордана для каждого корня.
Пример 8.6. Обратимся к системе управления из примера 8.5 и найдем уравнения состояния в канонической форме для разомкнутой системы. Характеристическое уравнение разомкнутой системы 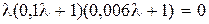 имеет три различных корня:
имеет три различных корня: 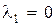 ,
, 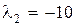 ,
, 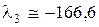 . Используя выражение
. Используя выражение 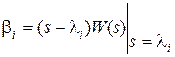 , находим величины
, находим величины  :
: 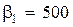 ,
, 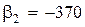 ,
, 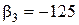 . Таким образом, уравнения состояния в канонической форме для разомкнутой системы имеют вид
. Таким образом, уравнения состояния в канонической форме для разомкнутой системы имеют вид
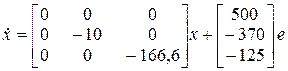 ,
,  .
.
С учетом уравнения замыкания 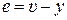 нетрудно получить следующие уравнения состояния замкнутой системы:
нетрудно получить следующие уравнения состояния замкнутой системы:
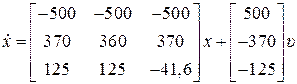 ,
, 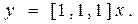 (8.26)
(8.26)
Сравнивая (8.21) и (8.26), видим, что одна и та же система описывается разными уравнениями состояния, которые эквивалентны между собой.
Дата добавления: 2015-02-07; просмотров: 1376;
