Z-преобразование
В данном разделе приводятся необходимые для дальнейшего рассмотрения сведения о математическом аппарате Z-преобразования. Более подробная информация содержится в [1].
Z-преобразованием (прямым) последовательности 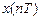 называют следующий ряд
называют следующий ряд
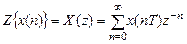 , (1.22)
, (1.22)
где 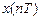 – оригинал – вещественная или комплексная последовательность, для которой выполняется условие (1.9);
– оригинал – вещественная или комплексная последовательность, для которой выполняется условие (1.9);
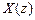 – z-изображение последовательности
– z-изображение последовательности 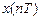 , результат Z-преобразования.
, результат Z-преобразования.
Z-преобразование однозначно связано с последовательностью 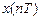 и справедливо только в области абсолютной сходимости ряда
и справедливо только в области абсолютной сходимости ряда
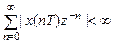 . (1.23)
. (1.23)
Z-преобразование (1.22) получено на основе известного дискретного преобразования Лапласа
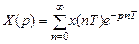
в результате замены переменных
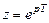 , (1.24)
, (1.24)
где p – оператор Лапласа
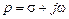 . (1.25)
. (1.25)
Определим взаимосвязь между комплексными p- и z-плоскостями.
Подставляя p (1.25) в (1.24), получаем
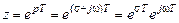 , (1.26)
, (1.26)
после чего, раскрывая 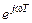 по формуле Эйлера
по формуле Эйлера
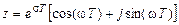 ,
,
имеем вещественную x и мнимую 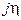 части комплексной переменной z (рис. 1.10):
части комплексной переменной z (рис. 1.10):
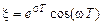 ; (1.27)
; (1.27)
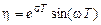 . (1.28)
. (1.28)
Комплексная переменная z может быть представлена в двух формах:
- алгебраической
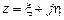 ; (1.29)
; (1.29)
- показательной
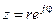 , (1.30)
, (1.30)
где радиус 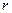 является модулем, а угол j – аргументом переменной z (1.29):
является модулем, а угол j – аргументом переменной z (1.29):
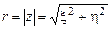 ; (1.31)
; (1.31)
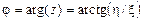 . (1.32)
. (1.32)
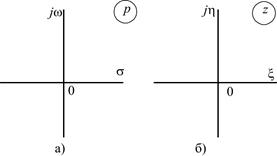
Рис. 1.10. Комплексные p- и z-плоскости
Соответственно, положение произвольной точки на комплексной z-плоскости может указываться:
- координатами (x;h) – в декартовой системе координат;
- полярными координатами (радиусом r и углом j) – в полярной системе координат.
Сопоставляя соотношения (1.26) и (1.30), выразим значения радиуса r и угла j через s и w соответственно:
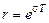 ; (1.33)
; (1.33)
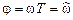 . (1.34)
. (1.34)
Равенство (1.34) указывает на то, что угол j точки на комплексной z-плоскости есть не что иное, как нормированная частота 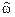 (1.8), измеряемая в радианах.
(1.8), измеряемая в радианах.
В силу периодичности экспоненты 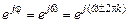 угол j (1.34) комплексной переменной z определяется с точностью до слагаемого 2pk, где k – любое целое число:
угол j (1.34) комплексной переменной z определяется с точностью до слагаемого 2pk, где k – любое целое число:
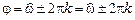 ,
,
однако, как правило, по умолчанию речь идет о главном значении аргумента из диапазона
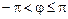 .
.
Дата добавления: 2015-02-10; просмотров: 2607;
