Обратное Z-преобразование
Обратное Z-преобразование определяется соотношением
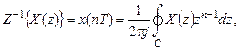
где 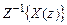 – символическое обозначение обратного Z-преобразования;
– символическое обозначение обратного Z-преобразования;
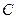 – любой замкнутый контур в области сходимости подынтегральной функции, охватывающий все ее особые точки (см. п. 1.4.2) и начало координат комплексной z-плоскости.
– любой замкнутый контур в области сходимости подынтегральной функции, охватывающий все ее особые точки (см. п. 1.4.2) и начало координат комплексной z-плоскости.
Существуют упрощенные способы вычисления обратного Z-преобразования, заменяющие непосредственное сложное вычисление интеграла по замкнутому контуру; наиболее простой из них основан на использовании таблицы соответствий (табл. 1.4), где последовательности представлены в нормированном времени (см. п. 1.1).
Поясним правило пользования табл. 1.4 на примерах.
Пример 1.6. Известно z-изображение
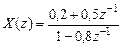 .
.
Требуется найти оригинал 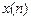 .
.
Решение. Представим дробно-рациональную функцию 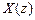 в виде суммы
в виде суммы
Таблица 1.4
Таблица соответствий
| № | Последовательность
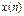
| z-изображение
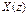
|
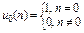
| 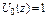
| |
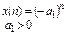
| 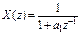
| |
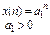
| 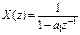
| |
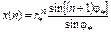
| 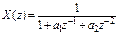 ,
где ,
где
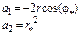
|
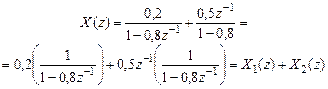 (1.38)
(1.38)
и, пользуясь свойством линейности Z-преобразования, определим оригинал 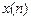 как сумму обратных Z-преобразований:
как сумму обратных Z-преобразований:
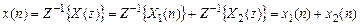 .
.
Оригинал
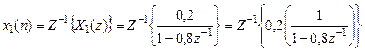 ,
,
согласно табл. 1.4 (столбец 3 при 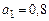 ), а также свойству линейности Z-преобразования равен
), а также свойству линейности Z-преобразования равен
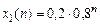 . (1.39)
. (1.39)
Оригинал
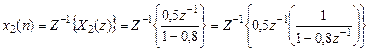
согласно табл. 1.4, (столбец 3 при 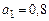 ), а также свойству линейности Z- преобразования и теореме о задержке равен
), а также свойству линейности Z- преобразования и теореме о задержке равен
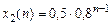 .
.
Искомый оригинал равен сумме последовательностей 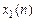 и
и 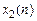 :
:
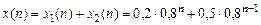 . (1.40)
. (1.40)
С учетом нулевых начальных условий оригинал 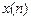 определяется следующим образом:
определяется следующим образом:
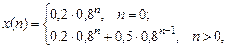
поскольку при 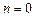 значение
значение 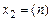 определяется в области отрицательного времени
определяется в области отрицательного времени
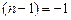
и, следовательно, при нулевых начальных условиях
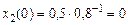 .
.
1.4.2. Передаточная функция. Соотношение вход/выход
Основной характеристикой ЛДС в z-областиявляется z-изображение импульсной характеристики 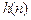
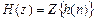 , (1.41)
, (1.41)
которое определяется по формуле прямого Z-преобразования (1.22)
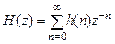 . (1.42)
. (1.42)
При известном z-изображении 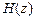 импульсная характеристика
импульсная характеристика 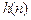 находится с помощью обратного Z-преобразования
находится с помощью обратного Z-преобразования
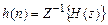 , (1.43)
, (1.43)
где 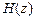 называют передаточной функцией (ПФ) ЛДС; это математическое определение ПФ.
называют передаточной функцией (ПФ) ЛДС; это математическое определение ПФ.
Соотношение вход/выход ЛДС во временной области описывалось с помощью формулы свертки, либо в виде разностного уравнения. Рассмотрим поочередно их отображение в z-области.
Формуле свертки (см. п. 1.3.1)
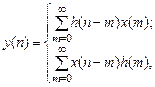
в z-области соответствует уравнение (см. п. 1.4.1)
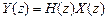 , (1.44)
, (1.44)
где 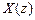 и
и 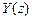 – z-изображения воздействия и реакции.
– z-изображения воздействия и реакции.
На основании (1.44) передаточную функцию можно представить как отношение
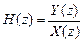 , (1.45)
, (1.45)
которое позволяет ее определить подобно передаточной функции линейных аналоговых систем.
Передаточной функцией 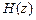 ЛДС называется отношение
ЛДС называется отношение
z-изображения реакции к z-изображению воздействия при нулевых начальных условиях.
Данное определение ПФ не противоречит приведенному математическому (1.42). Действительно, согласно определению, импульсная характеристика 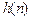 есть реакция на воздействие в виде цифрового единичного импульса
есть реакция на воздействие в виде цифрового единичного импульса 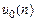 .
.
Подставив z-изображения данных воздействия и реакции в (1.45) и учитывая, что 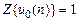 (см. табл. 1.4), получим определение ПФ (1.42):
(см. табл. 1.4), получим определение ПФ (1.42):
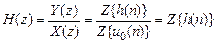 .
.
Разностному уравнению (1.15)
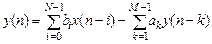
в z-области соответствует уравнение, которое можно получить, выполнив Z-преобразование правой и левой частей РУ:
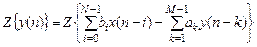 .
.
Используя свойства Z-преобразования (линейность и теорему о задержке), запишем
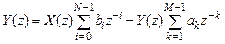 ,
,
откуда после приведения подобных имеем алгебраическое уравнение
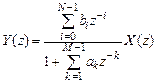 . (1.45а)
. (1.45а)
Разделив обе части этого уравнения на 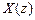 , получим передаточную функцию общего вида
, получим передаточную функцию общего вида
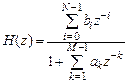 . (1.46)
. (1.46)
ПФ (1.46) представляет собой дробно-рациональную функцию, числитель и знаменатель которой являются многочленами относительно 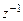 порядков
порядков 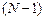 и
и 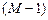 соответственно с вещественными коэффициентами
соответственно с вещественными коэффициентами 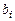 и
и 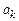 . Следовательно, ПФ зависит исключительно от внутренних параметров ЛДС (см. п. 1.3.2) и не зависит ни от воздействия, ни от реакции.
. Следовательно, ПФ зависит исключительно от внутренних параметров ЛДС (см. п. 1.3.2) и не зависит ни от воздействия, ни от реакции.
Порядком ПФ называют наибольшее из чисел 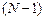 и
и 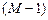 . Здесь и далее полагаем, что порядок многочлена числителя не превосходит порядка многочлена знаменателя:
. Здесь и далее полагаем, что порядок многочлена числителя не превосходит порядка многочлена знаменателя:
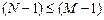 .
.
Передаточные функции 1-го и 2-го порядков описывают простейшие ЛДС, называемые звеньями 1-го и 2-го порядков соответственно.
Как любая дробно-рациональная функция, ПФ (1.46) характеризуется своими особыми точками (полюсами) и нулями.
Нулями ПФ называют значения z, при которых 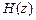 оказывается равной нулю.
оказывается равной нулю.
Особыми точками (полюсами) ПФ называют значения z, при которых знаменатель 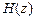 оказывается равным нулю [1].
оказывается равным нулю [1].
Картой нулей и полюсов называют изображение координат нулей (кружочками °) и полюсов (звездочками *) на комплексной z-плоскости. Как будет показано (см. пп. 1.5.5–1.5.6), такая карта является весьма важной графической характеристикой ЛДС.
1.4.3. Взаимосвязь передаточной функции
и разностного уравнения
Из сравнения передаточной функции (1.46) и соответствующего ей разностного уравнения (1.15) легко видеть, что:
- многочлен числителя ПФ связан с отсчетами воздействия 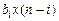 ; при этом величина задержки i отсчета
; при этом величина задержки i отсчета 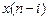 отображается степенью
отображается степенью 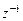 , а коэффициенты
, а коэффициенты 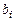 остаются неизменным; символически это соответствие можно записать следующим образом:
остаются неизменным; символически это соответствие можно записать следующим образом:
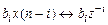 ,
, 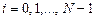 ;
;
- многочлен знаменателя ПФ связан с отсчетами реакции 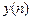 и
и 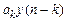 , при этом свободный член всегда равен 1:
, при этом свободный член всегда равен 1:
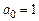 ,
,
так как в РУ он соответствует реакции 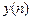 (см. п. 1.4.2);
(см. п. 1.4.2);
величина задержки k отсчета 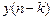 отображается степенью
отображается степенью 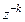 , а коэффициенты
, а коэффициенты 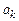 меняют знак; символически это соответствие можно записать следующим образом:
меняют знак; символически это соответствие можно записать следующим образом:
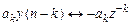 .
.
Пример 1.7. Дана передаточная функция общего вида. Записать соответствующее ей разностное уравнение:
- для звена 1-го порядка (числитель и знаменатель ПФ – многочлены 1-го порядка):
передаточной функции
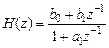 (1.47)
(1.47)
соответствует разностное уравнение
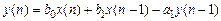 ; (1.48)
; (1.48)
- для звена 2-го порядка (числитель и знаменатель ПФ – многочлены 2-го порядка):
передаточной функции
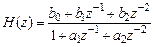 (1.49)
(1.49)
соответствует разностное уравнение
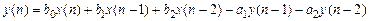 . (1.50)
. (1.50)
Звено называют базовым, если числитель его передаточной функции равен 1.
ПФ базовых звеньев 1-го и 2-го порядков имеют вид соответственно:
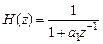 ;
; 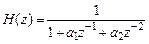 .
.
1.4.4. Передаточная функция
и импульсная характеристика звена 2-го порядка
Упрощенная методика определения импульсной характеристики 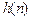 по заданной передаточной функции
по заданной передаточной функции 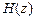 предполагает, что взаимосвязь между ИХ и ПФ базовых звеньев известна из таблицы соответствий (см. табл. 1.4), в предположении, что:
предполагает, что взаимосвязь между ИХ и ПФ базовых звеньев известна из таблицы соответствий (см. табл. 1.4), в предположении, что:
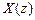 – передаточная функция
– передаточная функция 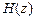 базового звена;
базового звена;
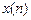 – импульсная характеристика
– импульсная характеристика 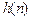 базового звена.
базового звена.
Следовательно, передаточной функции базового звена 1-го порядка
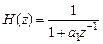
соответствует импульсная характеристика
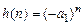 ,
,
а передаточной функции базового 2-го порядка
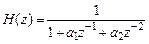
соответствует импульсная характеристика
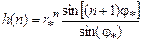 , (1.51)
, (1.51)
где 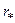 и j
и j 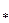 – радиус и угол комплексно-сопряженных полюсов
– радиус и угол комплексно-сопряженных полюсов
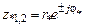 . (1.52)
. (1.52)
Значения 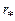 и j*и
и j*и 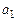 и
и 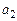 связаны между собой соотношениями (см. табл. 1.4)
связаны между собой соотношениями (см. табл. 1.4)
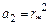 ; (1.53)
; (1.53)
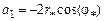 . (1.54)
. (1.54)
Напомним (см. рис. 1.11), что угол полюса j 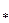 есть нормированная частота
есть нормированная частота 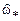 .
.
Здесь и в дальнейшем будем использовать индексы звездочка и кружок для обозначения полюса и нуля соответственно.
Для записи ИХ небазового звена 2-го порядка достаточно воспользоваться свойствами линейности Z-преобразования и теоремой о задержке.
Тогда передаточной функции небазового звена 2-го порядка
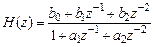
будет соответствовать импульсная характеристика небазового звена 2-го порядка
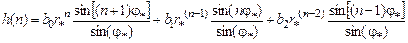 (1.55)
(1.55)
или с учетом нулевых начальных условий
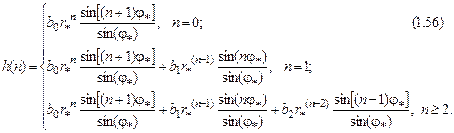
Дата добавления: 2015-02-10; просмотров: 3516;
