КИХ- и БИХ-системы

Рассмотрим особенности импульсных характеристик рекурсивных и нерекурсивных ЛДС. С этой целью приведем примеры вычисления ИХ по заданному разностному уравнению, решая его методом прямой подстановки при нулевых начальных условиях.

Пример 1.3. Вычислить импульсную характеристику нерекурсивной ЛДС второго порядка, соотношение вход/выход которой описывается разностным уравнением (1.20):

.

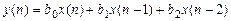Решение. Согласно определению ИХ – это реакция на цифровой единичный импульс (рис. 1.6), поэтому, выполнив замену

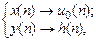(1.21)

перепишем РУ в виде

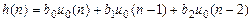
и вычислим отсчеты ИХ методом прямой подстановки при нулевых начальных условиях (см. п. 1.3.2):

;

;

;

;

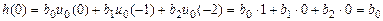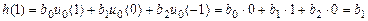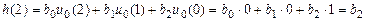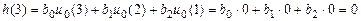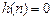при .

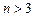Распространяя полученные результаты на ИХ нерекурсивной ЛДС произвольного порядка, можно сделать следующие выводы:

- импульсная характеристика нерекурсивной ЛДС имеет конечную длительность;

- значения отсчетов ИХ равны коэффициентам разностного уравнения

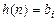, при .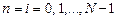

Поэтому нерекурсивные ЛДС называют системами с конечной импульсной характеристикой (КИХ-системами).

Пример 1.4. Вычислить импульсную характеристику рекурсивной ЛДС первого порядка, соотношение вход/выход которой описывается разностным уравнением

.

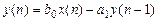Решение. Выполнив замену (1.21), перепишем РУ в виде

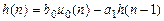
и вычислим отсчеты ИХ методом прямой подстановки при нулевых начальных условиях:

;

;

;

.

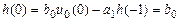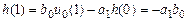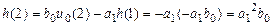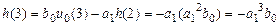Вычисления можно продолжать бесконечно по формуле

,

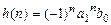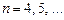
Распространяя полученные результаты на ИХ рекурсивной ЛДС произвольного порядка, можно сделать вывод: импульсная характеристика рекурсивной ЛДС имеет бесконечную длительность.

Поэтому рекурсивные ЛДС называют системами с бесконечной импульсной характеристикой (БИХ-системами).