Вычисление реакции методом прямой подстановки

n	Воздействие	Реакция
	x(0) = 1	y(0) = x(0) –0,5y(–1) = 1 – 0,5·0 = 1
	x(1) = 0,1	y(1) = x(1) – 0,5y(0) = 0,1 – 0,5·1 = 0,1 – 0,5= –0,4
	x(2) =0,01	y(2) = x(2) – 0,5y(1) = 0,01 – 0,5·(–0,4) = 0,01 + 0,2=0,21
	x(3) = 0,001	y(3) = x(3) – 0,5y(2) = 0,001 – 0,5·0,21 = 0,001 – 0,105 = = –0,104
	x(4) = 0,0001	y(4) = x(4) – 0,5y(3) = 0,0001 – 0,5·(–0,104) = = 0,0001+ 0,052 = 0,0521

1.3.3. Рекурсивные и нерекурсивные
линейные дискретные системы

Линейная дискретная система называется рекурсивной, если хотя бы один из коэффициентов a_k разностного уравнения (1.15) не равен нулю:

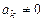хотя бы для одного из значений k.

Порядком рекурсивной ЛДС называют порядок РУ (1.15), т. е. .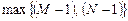

Согласно (1.15) реакция y(n) рекурсивной ЛДС в каждый момент времени n определяется:

- текущим отсчетом воздействия x(n);

- предысторией воздействия ;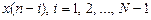

- предысторией реакции .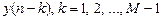

Примеры разностных уравнений рекурсивной ЛДС:

- первого порядка

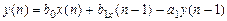; (1.16)

- второго порядка

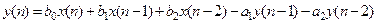.(1.17)

Линейная дискретная система называется нерекурсивной, если все коэффициенты 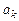разностного уравнения (1.15) равны нулю:

, .

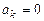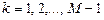Для нерекурсивной ЛДС разностные уравнения (1.14)–(1.15) принимают вид соответственно

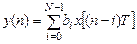; (1.18)

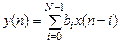. (1.19)

Порядок нерекурсивной ЛДС равен .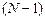

Согласно РУ (1.19) реакция 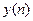нерекурсивной ЛДС в каждый момент времени n определяется:

- текущим отсчетом воздействия ;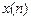

- предысторией воздействия .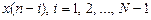

Пример РУ нерекурсивной ЛДС второго порядка:

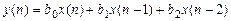. (1.20)