Алгоритмы вывода прямой линии

Рассмотрим растровые алгоритмы для отрезков прямой линии. Предположим, что заданы координаты ( x1, yl - х2, у2) концов отрезка прямой. Для вывода линии необходимо закрасить определенным цветом все пикселы вдоль линии. Для того чтобы закрасить любой пиксел, необходимо знать его координаты.

Наиболее просто нарисовать отрезок горизонтальной линии.

Вычисление текущих координат пиксела выполняется как приращение по x (необходимо, чтобы х1 ≤ х2), а вывод пиксела обеспечивается специальной функцией.

Аналогично рисуется отрезок вертикали.

В цикле вывода горизонтального и вертикального отрезков выполняются простейшие операции — приращение на единицу, проверка на "< =" и запись пиксела в буфер растра. Поэтому операция рисования таких отрезков выполняется быстро и просто. Ее используют как базовую операцию для других операций, например, в алгоритмах заполнения полигонов.

Можно задать такой вопрос: какая линия рисуется быстрее — горизонталь или вертикаль? На первый взгляд — одинаково быстро. Если учитывать только математические аспекты, то скорость должна быть одинаковой при равной длине отрезков линий, поскольку в обоих случаях выполняется одно и то же количество одинаковых операций. Однако если кроме вычисления координат анализировать вывод пикселов в конкретный растр, то могут быть отличия. В растровых системах рисование пиксела обычно означает запись одного или нескольких битов в память, где сохраняется растр. И здесь уже не все равно — по строкам или по столбцам заполняется растр. Необходимо учитывать логическую организацию памяти компьютера, в которой хранятся биты или байты растра. Даже для компьютеров одного типа (например, персональных компьютеров) для разных поколений процессоров и памяти скорость записи по соседним адресам может существенно отличаться от скорости записи по не соседним адресам. В особенности это заметно, если для растра используется виртуальная память с сохранением отдельных страниц на диске и (или) в оперативной памяти (RAM). При работе графических программ в среде операционной системы Windows часто случается так, что горизонтали рисуются быстрее вертикалей, так как в каждой странице памяти сохраняются соседние байты — пикселы вдоль горизонтали растра. Подобный эффект также имеет место при использовании кэш-памяти. А может быть, что RAM достаточно, и даже весь растр размещается в кэше, а скорости рисования все же отличаются. Например, если используется черно-белый растр в формате один бит на пиксел, то для вертикали битовая маска одинакова для всех пикселов линии, а для горизонтали маску нужно изменять на каждом шаге. Здесь необходимо заметить, что рисование черно-белых горизонталей можно существенно ускорить, если записывать сразу восемь соседних пикселов — байт в памяти.

Горизонтали и вертикали представляют собой частный случай линий. Рассмотрим линию общего вида. Для нее также необходимо вычислять координаты любого пиксела. Известны несколько методов расчетов координат точек линии.

Прямое вычисление координат

Пусть заданы координаты конечных точек отрезка прямой. Найдем координаты точки внутри отрезка.

Запишем соотношения катетов для подобных прямоугольных треугольников:

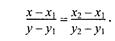
Перепишем это соотношение как х =f(y):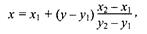

а также как

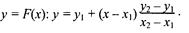
В зависимости от угла наклона прямой выполняется цикл по оси х или по у(рис. 3. 28).

Рис. 3.28. Отрезок прямой.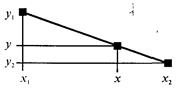

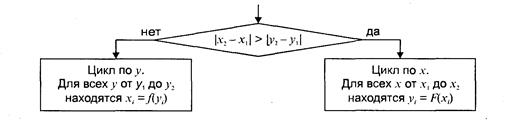
Рис. 3.29. Общая схема алгоритма вывода отрезка прямой линии

Положительные черты прямого вычисления координат.

1. Простота, ясность построения алгоритма.

2. Возможность работы с нецелыми значениями координат отрезка. (Как вы считаете, в каком варианте из четырех корректно вычисляются координаты пикселов, если х1, у1, х2 и у2 — дробные?)

Недостатки.

1. Использование операций с плавающей точкой или целочисленных операций умножения и деления обуславливает маленькую скорость. Однако это зависит от процессора, и для разных типов компьютеров может быть по-разному. В современных компьютерах, в которых процессоры используют эффективные средства ускорения (например, конвейер арифметических операций с плавающей точкой), время выполнения целочисленных операций уже не намного меньше. Для старых компьютеров разница могла составлять десятки раз, поэтому и старались разрабатывать алгоритмы только на основе целочисленных операций.

2. При вычислении координат добавлением приращений может накапливаться ошибка вычислений координат.

Последнюю разновидность прямого вычисления координат, рассмотренную здесь, можно было бы назвать "инкрементной". Но такое название получили алгоритмы другого типа.