Кривая Безье

Разработана математиком Пьером Безье. Кривые и поверхности Безье были использованы в 60-х годах компанией "Рено" для компьютерного проектирования формы кузовов автомобилей. В настоящее время они широко используются в компьютерной графике.

Кривые Безье описываются в параметрической форме: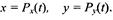

Значение t выступает как параметр, которому соответствуют координаты отдельной точки линии. Параметрическая форма описания может быть удобнее для некоторых кривых, чем задание в виде функции у =ƒ(х), поскольку функция ƒ(х) может быть намного сложнее, чем P_x(t) и P_y(t), кроме того, ƒ(x) может быть неоднозначной.

Многочлены Безье для Р_x и Р_y имеют такой вид:

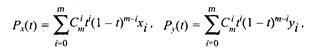
где x_i и y_i — координаты точек-ориентиров Р_i, а величины 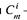— это известные из комбинаторики, так называемые сочетания (они также известны как коэффициенты бинома Ньютона):

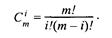
Значение да можно рассматривать и как степень полинома, и как значение, которое на единицу меньше количества точек-ориентиров.

Рассмотрим кривые Безье, классифицируя их по значениям т.

т = 1 (по двум точкам)

Кривая вырождается в отрезок прямой линии, которая определяется конечными точками Р_о и Р₁, как показано на рис. 3. 30:

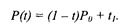
m=2 (по трем точкам, рис. 3. 32):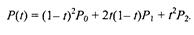

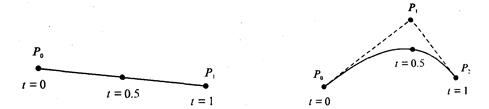
Рис. 3.32. Кривая Безье (m=1) Кривая Безье (m=2)

т = 3 (по четырем точкам, кубическая, рис 3.33). Используется довольно часто, в особенности в сплайновых кривых:

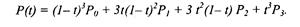
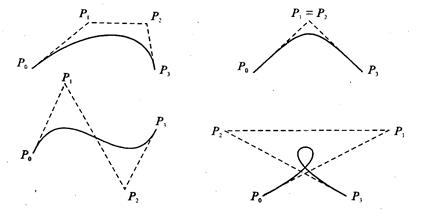
Рис. 3.33. Кубические кривые Безье (m=3)

Геометрический алгоритм для кривой Безье

Этот алгоритм позволяет вычислить координаты (х, у) точки кривой Безье по значению параметра t.

1. Каждая сторона контура многоугольника, который проходит по точкам-ориентирам, делится пропорционально значению t.

2.Точки деления соединяются отрезками прямых и образуют новый многоугольник. Количество узлов нового контура на единицу меньше, чем количество узлов предшествующего контура.

3. Стороны нового контура снова делятся пропорционально значению t. И так далее. Это продолжается до тех пор, пока не будет получена единственная точка деления. Эта точка и будет точкой кривой Безье (рис. 3.34).

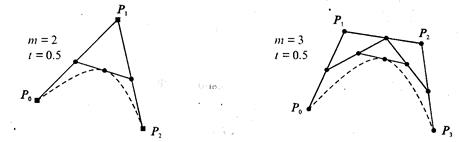
Рис. 3.34. Геометрический алгоритм для кривых Безье