Автоматизированное проектирование дорог с помощью кривых Безье.

В 1970 г. Пьер Безье (французский математик) подобрал составляющие параметрического кубического многочлена таким образом, что их физический смысл стал очень наглядным и весьма подходящим для решения многих прикладных задач, в том числе и для целей проектирования дорог по принципу "тангенциального трассирования".

Формула Безье для кубического многочлена (n = 3) имеет следующий вид.

Пусть r_i = 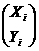, i = 0, 1, 2, 3, тогда для 0 ≤ t ≤ 1:

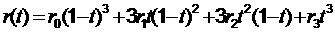
или в матричной форме:

.

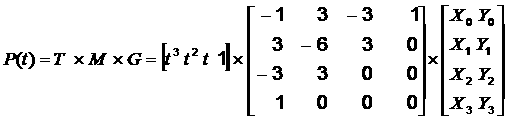Матрица M называется базисной матрицей кубической кривой Безье.

Кривая, представленная в форме Безье, проходит через точки r₀ и r₃, имеет касательную в точке r₀, направленную от r₀ к r₁, и касательную в точке r₃, направленную от r₂ к r₃.

Прямые Р₀Р₁, Р₁Р₂ и Р₂Р₃ образуют фигуру, называемую характеристической (определяющей) ломаной, которая и предопределяет очертания кривой Безье (рис. 2.6).

Чтобы построить кривую, задают точки Р₀ и Р₃, через которые должна проходить кривая, затем на желаемых касательных к этой кривой в точках Р₀ и Р₃ задают точки Р₁ и Р₂. Изменяя длины отрезков Р₀Р₁ и Р₂Р₃ варьируют очертаниями кривой, придавая ей желаемую форму.

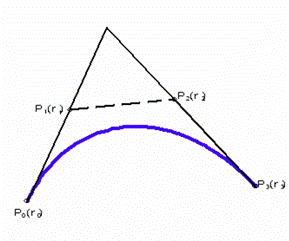
Рис. 2.6. Сегмент кубической кривой Безье

Главной контролируемой величиной при проектировании кривых в плане является радиус кривизны. Для того, чтобы вычислять радиус кривизны в каждой точке кривой, необходимо знать значения первой и второй производных радиуса-вектора точки. Для кубической кривой Безье первая и вторая производные вычисляют по нижеприведенным формулам:

, .

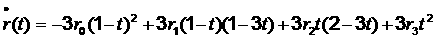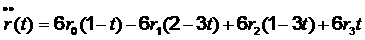Тогда кривизна (величина, обратная радиусу кривизны) вычисляется по формуле: .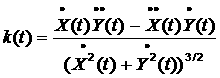

Помимо кривой Безье 3-го порядка (кубической) для целей трассирования дорог возможно применение также кривых Безье 2-го, 4-го и 5-го порядков. Соответствующие формулы для вычисления радиусов-векторов (и их производных) для этих кривых приведены ниже.

Кривая Безье 2-го порядка: .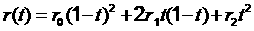

Кривая Безье 4-го порядка: .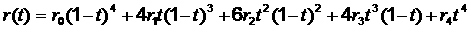

Кривая Безье 5-го порядка: .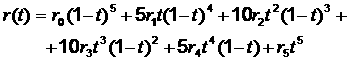

Объединением элементарных кривых Безье γ⁽¹⁾, γ⁽²⁾,…, γ^(l), у которых концевая точка кривой γ⁽ⁱ⁾, i = 1, 2,…, l–1, совпадает с начальной точкой кривой γ⁽ⁱ⁺¹⁾, получается составная кривая Безье. Если каждая кривая γ⁽ⁱ⁾ задается параметрическим уравнением вида

r = r⁽ⁱ⁾ (t), 0 ≤ t≤ 1,

то это условие записывается так:

r⁽ⁱ⁾ (1) = r⁽ⁱ⁺¹⁾ (0), i = 1, 2,…, l–1.

В частности, для того, чтобы касательная составной кривой Безье, определяемой набором точек P₀, P₁, …, P_m, изменялась непрерывно вдоль этой кривой, необходимо, чтобы тройки вершин P_3i-1, P_3i, P_3i+1 (i ≥ 1) были коллинеарными, то есть лежали на одной прямой (см. рис. 2.7).

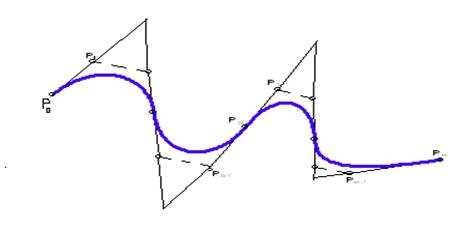
Рис. 2.7.Составная кубическая кривая Безье

Пространственные кривые Безье.Выше, в рассуждениях о Безье-кривых понималось плоское расположение опорных точек трассы и, соответственно, рассматривалось представление только плоских кривых. В общем случае опорные точки характеристической ломаной Безье задаются точками трехмерного пространства P_i(x_i, y_i, z_i), i = 0, 1 ,…, m.

Тогда пространственная кривая Безье степени m определяется уравнением, имеющим следующий вид:

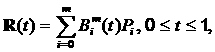
где 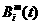– многочлены Бернштейна.

Матричная запись параметрических уравнений, описывающих пространственную кривую Безье, имеет вид:

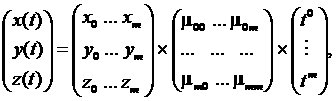0≤ t ≤ 1,

где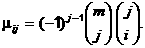

Более подробное изложение пространственного трассирования дорог приведено в гл. 5.

Методическое обеспечение – совокупность методических материалов, способствующих функционированию САПР.

Профессиональные САПР имеют, как правило, методическое сопровождение в виде "Справочных руководств" в бумажном виде. Главное меню таких систем также содержит раздел Справка (Помощь), в котором представлено описание основных проектных процедур.

В процессе эксплуатации САПР накапливается опыт рациональной выработки проектных решений на основе всей совокупности инструментальных средств системы. Этот опыт, как правило, излагается в форме "Практических руководств (пособий)" и способствует повышению эффективности и качества инженерного труда