Триангуляция Делоне и способы ее редактирования

Массив точек для регулярных моделей может быть представлен в следующем виде:

F, m, n, X₀, Y₀, Z₁₁,…, Z_1m,…, Z_nm,

где F –шаг сетки; m –число точек по горизонтали; n –число точек по вертикали; X₀, Y₀–координаты начальной точки сетки,Z₁₁,…,Z_1m,,…,Z_nm –отметки точек в узлах сетки.

Таким образом, для однозначного представления регулярной сетки размерностью mn требуется хранить всего mn+5 чисел. Однако для адекватного представления поверхности с заданной точностью требуется высокая плотность точек, что сопряжено со значительной многодельностью работ по подготовке исходной информации. К тому же, в виду ограниченности быстродействия компьютеров и массивов обрабатываемых данных приходится выбирать между точностью представления (размером ячейки) и размером обрабатываемой поверхности.

Для нерегулярных моделей массив точек описывается последовательностью:

X_i, Y_i, Z_i, T_i, R_i, L_i,

где X_i, Y_i, Z_i –координаты i-той точки (массив i =1,…,k); T_i, R_i, L_i – соответственно принадлежность i-той точкиT_i треугольнику, связь i-той точки с R_iиL_i точками в треугольнике.

Размерность нерегулярной сетки составляет 6k, что почти в 6 раз выше размерности регулярной сетки, но, в тоже время, для адекватного отображения поверхности требуется существенно меньшее количество точек.

Задача построения поверхности способом триангуляции является одной из базовых в вычислительной геометрии. К ней сводятся многие другие, связанные с моделированием поверхностей и решением пространственных задач в машинной графике, системах автоматизированного проектирования и геоинформационных системах.

Задачей построения триангуляции по заданному набору точек называется задача соединения точек непересекающимися отрезками так, чтобы образовалась триангуляция. Эта задача не является однозначной, поэтому возникает вопрос, какая из двух различных триангуляций лучше (оптимальна)?

Рассмотрим некоторые алгоритмы построения триангуляции.

Триангуляция Делоне, названная в честь советского математика Б. Н. Делоне (1934 г.), основана на ряде практических свойств:

· триангуляция, удовлетворяет условию Делоне, если внутрь окружности, описанной вокруг любого построенного треугольника, не попадает ни одна из заданных точек триангуляции;

· пара соседних треугольников триангуляции удовлетворяет условию Делоне, если этому условию удовлетворяет триангуляция, составленная только из этих двух треугольников;

· триангуляции удовлетворяет условию Делоне, если этому условию удовлетворяет триангуляция, составленная только из этого треугольника и трех его соседей (если они существуют).

· триангуляция Делоне обладает максимальной суммой минимальных углов всех своих треугольников среди всех возможных триангуляций;

· триангуляция Делоне обладает минимальной суммой радиусов окружностей, описанных около треугольников, среди всех возможных триангуляций.

Триангуляцию Делоне можно получить из любой другой триангуляции по тому же массиву точек, последовательно перестраивая пары соседних треугольников СABC и DBCD, не удовлетворяющих свойствам Делоне, в пары треугольников DABD и DACD (рис. 4.8). Такую операцию называют флип.

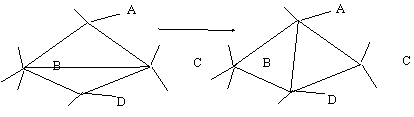
Рис. 4.8. Перестроение треугольников (флип)

Важно, что операцию флип можно применять не только в составе алгоритма построения оптимальной триангуляции поверхности, но и в составе инструментов диалогового ее редактирования, что позволяет получать желаемые для проектировщика свойства этой поверхности.

Другим алгоритмом, который достаточно просто и наглядно демонстрирует последовательность построения оптимальной триангуляции, является жадный алгоритм. В качестве условия оптимизации здесь принята минимальная сумма длин всех ребер среди всех возможных триангуляций, построенных на тех же исходных точках. Этот алгоритм выполняется всего в 2 шага.

· Генерируется список всех возможных отрезков (рис.а), соединяющих пары исходных точек, и он сортируется по длинам отрезков.

· Начиная с самого короткого, последовательно выполняется вставка отрезков в триангуляцию. Если отрезок не пересекается с другими ранее вставленными отрезками, то он вставляется, иначе – отбрасывается (рис.б).

В триангуляции можно выделить 3 основных вида объектов: узлы(точки, вершины), ребра (отрезки) и треугольники. В процессе выполнения конкретных проектных задач возникает необходимость выполнения вычислительных операций с этими объектами. Приведем лишь некоторые из возможных операций.

· Треугольник  узлы: требуется для получения высотной отметки проектной точки, расположенной внутри конкретного треугольника. Для этого устанавливаются координаты узлов (вершин) этого треугольника, а далее - в уравнение плоскости, проходящей через эти три узла, подставляются координаты x,y проектной точки.

· Узел  ребра: требуется для анализа водоотвода на рассматриваемой поверхности. По узлу устанавливается список всех смежных ребер, каждое из которых анализируется на возможность "перелива" воды.

· Треугольник  треугольник: требуется для построения изолиний рассматриваемой поверхности. По треугольнику устанавливается список соседних с ним треугольников и на них вычисляется геометрическое место точек с заданной высотной отметкой.