При цифровом моделировании местности могут использоваться регулярные, нерегулярные и статистические ЦММ.

Цифровое и математическое моделирование существенно изменило методы изысканияи проектирования строительных объектов.

АППРОКСИМАЦИЯ (от лат. approximo - приближаюсь), замена одних математических объектов (напр., чисел или функций) другими, более простыми и в том или ином смысле близкими к исходным (напр., кривых линий близкими к ним ломаными).

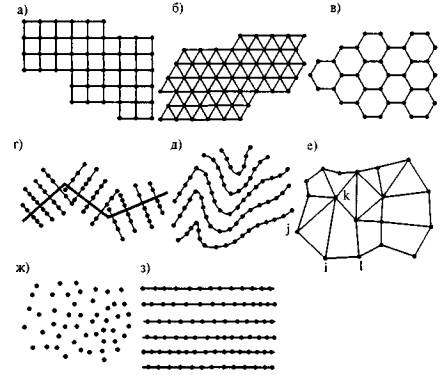
Рис. Виды цифровых моделей местности:
а - в узлах правильных прямоугольных сеток; б - в узлах треугольных сеток; в - в узлах шестиугольных сеток (регулярные); г - нерегулярные-на поперечниках к магистральному ходу; д - на горизонталях; е – нерегулярные на структурных линиях; ж - статистическая; з - на линиях, параллельных оси фотограмметрических координат.

В регулярных моделях - точки с известными пространственными координатами располагаются в вершинах сетки либо квадратов, либо прямоугольников, либо равносторонних треугольников. Существуют также цифровые модели в виде системы поперечных профилей, проведенных через определенные расстояния вдоль заданной линии (например, оси трассы). По регулярным моделям высотное положение в любой точке местности, как правило, определяется линейной интерполяцией высот внутри заданного квадрата, прямоугольника или треугольника. Основными недостатками таких моделей являются неэффективное расположение точек, так как не на всех участках требуется одинаковая плотность сетки, и повышенные трудозатраты при разбивке узловых точек на местности. Регулярные модели находят применение в тех случаях, когда требуется повышенная точность съемки, например, при проектировании аэродромов.

В статистических цифровых моделях точки с известными пространственными координатами располагаются на структурных линиях рельефа, местах изменения углов наклона склонов, на характерных линиях дороги, урезах рек. Изменение отметок вдоль структурной линии описывается полиномиальной зависимостью(полином - это многочлен, т.е. выражение вида Ax^ky¹... w^m + Вxⁿy^p... wⁿ +…, где x, y, ..., w — переменные, а А, В, ..., D (коэффициенты полинома) и k, l, ..., t (показатели степеней — целые неотрицательные числа) — постоянные. Отд. слагаемые вида Ax^ky¹... w^m - наз. членами полинома. Порядок членов, а также порядок множителей в каждом члене можно менять произвольно; точно так же можно вводить или опускать члены с нулевыми коэффициентами, а в каждом отд. члене — степени с нулевыми показателями). Полиномиальное распределение - совместное распределение вероятностей случайных величин, каждая из которых есть число появлений одного из нескольких взаимно исключающих событий при повторных независимых испытаниях. По сравнению с регулярной структурная цифровая модель требует меньшую плотность исходных точек и при линейной интерполяции является весьма эффективной для описания поверхности городских дорог.
В нерегулярных цифровых моделях точки могут располагаться без какой-либо системы, но с заданной плотностью. Эти модели являются самыми универсальными и получили в настоящее время наиболее широкое распространение.
В современных программных продуктах цифровые модели рельефа создаются на основе съемочных точек и структурных линий, описывающих изломы естественного (овраги, урезы рек) или искусственного происхождения. При этом образуется сеть, состоящая из треугольников, вершинами которых являются съемочные точки. Это позволяет вычислять высотные отметки точек с известными координатами в плане, строить разрезы поверхности земли по заданной линии, отображать рельеф при помощи горизонталей.