Оценка устойчивости по импульсной характеристике

Существуют два критерия устойчивости ЛДС. Один из них позволяет оценить устойчивость ЛДС по ее импульсной характеристике во временной области, другой – по z-изображению этой характеристики в z-области (см. п. 1.4). Выбор критерия зависит от удобства его практического использования.

Критерий, позволяющей оценить устойчивость ЛДС по ее импульсной характеристике, формулируется следующим образом: для того чтобы ЛДС была устойчива, необходимо и достаточно выполнения условия абсолютной сходимости ряда

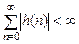. (1.21а)

Данный критерий устойчивости свидетельствует о том, что нерекурсивные ЛДС (КИХ-системы) всегда устойчивы, поскольку их импульсная характеристика конечна.

Прежде чем делать вывод об устойчивости рекурсивных ЛДС, рассмотрим простой пример.

Пример 1.5. Определить, устойчива ли рекурсивная ЛДС, импульсная характеристика которой описывается дискретной экспонентой (1.6)

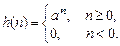
Решение.Подставив данную ИХ в правую часть критерия (1.21а), получим ряд

,

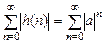представляющий собой сумму бесконечной геометрической прогрессии

, .

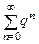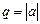Как известно, сумма такого ряда в области сходимости, т. е. при 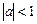, имеет конечный предел, равный

.

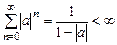В этом случае импульсная характеристика представляет собой затухающую экспоненту (см. рис. 1.3), а ЛДС согласно критерию (1.21а) является устойчивой.

Вне указанной области, т. е. при 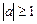, сумма бесконечной геометрической прогрессии не имеет конечного предела, ряд является расходящимся

,

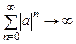а ЛДС по критерию (1.21а) – неустойчивой.

В общем случае относительно устойчивости БИХ-систем можно сделать следующие выводы:

- рекурсивные ЛДС (БИХ-системы) требуют проверки на устойчивость,

- импульсная характеристика устойчивой ЛДС имеет характер затухающей функции времени.

1.4. Описание линейных дискретных систем
в z-области

В п. 1.3 рассматривалось описание ЛДС во временной области: импульсная характеристика и соотношение вход/выход в виде формулы свертки либо разностного уравнения. Здесь рассматривается их отображение в z-области.

Описание ЛДС в z-области позволяет:

- ввести фундаментальное для теории линейных систем понятие передаточной функции;

- перейти от разностных уравнений к алгебраическим;

- упростить анализ устойчивости;

- обеспечить автоматический переход к частотным характеристикам и многое другое.

Прежде чем перейти к описанию ЛДС в z-области, рассмотрим математический аппарат Z-преобразования.