Критическое равновесие трещины

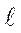Рассмотрим бесконечную пластину единичной толщины с централь-ной поперечной трещиной 2 , на которую действуют напряжения s (рис.4.7). Края пластины неподвижны. Необходимо определить величину напряжения, при котором трещина приходит в движение, и энергию W, необходимую для её распространения.

а - пластина с трещиной и с неподвижными краями;

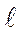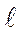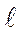б– энергия упругих деформаций пластины с трещиной длиной (1) и + ∆ (2)

Рисунок 4.7 – Растянутая пластина с трещиной длиной 2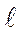

Запасенная в пластине упругая энергия представлена площадью тре - угольника ОАВ (рис.4.7,б). Если длина трещины увеличится на величину ∆ 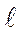, то жесткость пластины уменьшится (линия ОС), т.е. нагрузка неско- лько уменьшится, так как края пластины неподвижны.

Таким образом, запасённая в пластине упругая энергия уменьшится до величины, равной площади треугольника ОСВ, то есть увеличение дли-ны трещины от 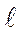до 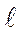+ ∆ 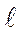высвободит упругую энергию, равную пло-щади треугольника ОАС.

Если пластина нагружается до более высокого напряжения, то при увеличении длины трещины на величину ∆ 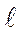высвободится большая энергия. Треугольник ОДЕ представляет собой энергию, выделенную при распространении трещины.

Для того, чтобы трещина смогла продвинуться на величину ∆ 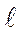(рис.4.8), необходимо разрушить межатомные связи на длине ∆ 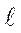, для че-го необходимо затратить определенную работу U. Напряженный металл в единице объема при одноосном растяжении напряжениями s содержит потенциальную энергию

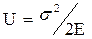. (4.11)

На рисунке 4.8 приведена графическая зависимость критического напряжения от критической длины трещины: .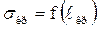

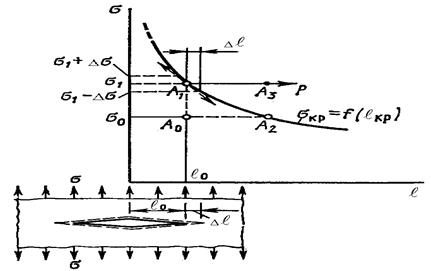
Рисунок 4.8 – Кривая критического равновесия трещины

В точке А_о, которая лежит ниже кривой, действуют напряжения s_о. Тогда любые случайные изменения в напряжениях s+Ds или в длине тре-щины 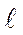+D 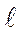не вызовут рост трещины, так как не будет выполняться энергетическое условие G = W и выделенной энергии G будет недоста-точно, чтобы компенсировать затраты работы на разрушение. При возрас-тании напряжения до s₁ точка А₁ окажется на кривой 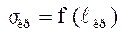. Здесь теоретически возможен медленный рост трещины с движением точ-ки А₁ вниз кривой так, чтобы увеличению длины ∆ 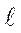строго соответство-вало снижение напряжений s - Ds и выполнялось бы энергетическое усло-вие dЭ + dА = 0 и трещина развивалась бы монотонно. Но это равновесие неустойчиво. Обычно в этих условиях нагрузка и напряжение s₁ остаются на постоянном уровне. Точка А₁ двигается по горизонтали в направлении точки А₃, выделяемая энергия dЭ превосходит затрачиваемую работу dА и возникает процесс разрушения. Увеличение напряжений s₁ + Ds требует даже "закрытия" трещины на длину ∆ 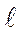, чтобы точка оставалась на кривой и выполнялось энергетическое равновесие. Но так как это невозможно, то возникает лавинообразное распространение трещины. Аналогичная ситуа-ция возникает, если за счет подрастания трещины система переходит из точки А₀ в точку А₂ при s₀ = const. Таким образом, данная кривая опре-деляет момент возникновения неустойчивости в равновесии трещины, ког-да любые случайные изменения напряжения или длины трещины вызовут ее рост, называется кривой А. Гриффитса. Критическое равновесие трещи-ны пределяется критическим коэффициентом интенсивности напряжений К, так как он знаменует потерю устойчивости равновесия системы.