В материале хрупкой зоны
Рассмотрим условие распространения трещины в случае наличия в материале хрупкойзоны 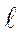 0 (рис.4.13).
0 (рис.4.13).

а б
Рисунок 4.13 - Схема, иллюстрирующая высвобождение и поглощение энергии при движении трещины в металле с хрупкой зоной 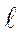 0
0 
Трещина, распространяясь по хрупкой зоне, затрачивает на свое рас-пространение ничтожно малое количество энергии. Освобождаемая избы-точная энергия накапливается в виде кинетической энергии движущихся частиц металла. Затем эта энергия расходуется на продвижение трещины в область металла с высокими пластическими свойствами. Размеры трещины достигают критических величин, после чего разрушение охватывает боль-шие участки. Кривая 1– высвобождаемая энергия при движении трещины. Ломаная линия ОАВ - затраты энергии на пластическую деформацию ме-талла при движении трещины. На участке 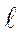 0 они близки к нулю. На учас-тке АВ – линейный рост затрат энергии на движение трещины по вязкому участку. Однако линия АВ не пересекает кривую 1- это означает, что ко-личество освобождающейся энергии больше израсходованной и трещина будет двигаться без остановки. Если металл за пределами зоны
0 они близки к нулю. На учас-тке АВ – линейный рост затрат энергии на движение трещины по вязкому участку. Однако линия АВ не пересекает кривую 1- это означает, что ко-личество освобождающейся энергии больше израсходованной и трещина будет двигаться без остановки. Если металл за пределами зоны 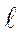 0 имеет очень высокие пластические свойства (линия АС), то трещина может оста-новиться в точке Е (рис. 4.13, а).
0 имеет очень высокие пластические свойства (линия АС), то трещина может оста-новиться в точке Е (рис. 4.13, а).
Допустим, что в пластине (рис.4.13, б) движение трещины идет без затрат энергии и трещина может распространиться до размера 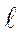 1. Полная энергия, которая освободится на участке
1. Полная энергия, которая освободится на участке 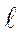 1,
1,
 ,
,
а затраты энергии на ее распространение
Uр= ( 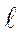 1-
1- 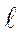 0) G,
0) G,
где G – энергия, затрачиваемая на единицу длины трещины в вяз-ком металле.
Пусть 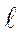 1 является критической длиной для данного значения G. Тогда
1 является критической длиной для данного значения G. Тогда 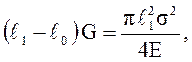 (4.25)
(4.25)
откуда 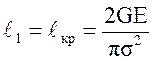 ,а
,а 
Подставляя значения 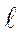 1 и G в выражение (4.25), получим:
1 и G в выражение (4.25), получим:
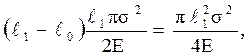
откуда 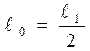 .(4.26)
.(4.26)
Таким образом, достаточно иметь хрупкую зону 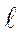 0, по длине в два раза меньшую критической длины трещины
0, по длине в два раза меньшую критической длины трещины 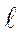 1, чтобы разрушение, воз-никнув, не прекратилось, а развивалось бы как нестабильное. Если бы бы-ла трещина длиной
1, чтобы разрушение, воз-никнув, не прекратилось, а развивалось бы как нестабильное. Если бы бы-ла трещина длиной 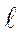 0, то она вела бы себя как стабильная и не развива-лась бы, так как критический размер
0, то она вела бы себя как стабильная и не развива-лась бы, так как критический размер 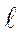 1 в два раза больше, чем
1 в два раза больше, чем 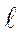 0.
0.
Дата добавления: 2015-01-10; просмотров: 991;
