Энергетическое условие А. Гриффитса

Практика эксплуатации металлоконструкций свидетельствует, что отдельные их элементы со временем могут разрушаться вследствие кон-центрации напряжений, дефектов технологии обработки и сборки, влияния среды, что приводит к возникновению и постепенному развитию трещины. Иногда деталь может использоваться почти на протяжении всего времени эксплуатации при наличии трещины. Таким образом, практически важно не столько наличие трещины, как скорость ее распространения в тех или иных условиях. В связи с этим одной из основных задач механики разрушения является изучение прочности тел с трещинами с учетом геометрии трещин и влияния на развитие трещины разных условий эксплуатации.

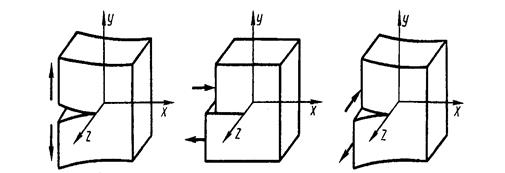
Различают три простейших типа развития трещин с точки зрения смещения их берегов один от другого в соответствии с действием различ-ных внешних нагрузок (рис.4.9).

При деформации растяжения (рис.4.9,а) возникает трещина отры-ва, когда ее поверхности смещаются в направлениях, перпендикулярных к поверхности трещины; при деформации поперечного сдвига (рис.4.9,б) по-верхности берегов трещины смещаются поперек ее передней кромки; при нагрузке, показанной на рис.4.9, в, образовываются трещины продольного сдвига, при котором точки поверхности трещины смещаются вдоль перед-ней кромки.

.

а б в

Рисунок 4.9 - Типы развития трещин в соответствии с действием различных внешних нагрузок

А. Гриффитс рассмотрел условия развития единичной трещины в пластине при ее растяжении и хрупком разрушении (см.рис.4.9,а), связан-ном с возникновением в материале трещин, вызванных дефектами в струк-туре материала, состоянием поверхности детали вследствие обработки или коррозии, действием повторно-статических нагрузок. Трещины, которые возникли, сначала развиваются во времени медленно, а затем - быстро. Развитие трещин со временем может происходить и при постоянной наг-рузке.

Из теории трещин известно, что для расширения трещины необходи-мо затратить определенную работу на преодоление сил взаимодействия со-седних частиц материала. Плотность поверхностной энергии W – это рабо-та, которая необходима для образования единицы новой поверхности, оп-ределяется экспериментально, для разных материалов будет разная и счи-тается константой материала. Тело предполагается идеально хрупким, т.е. энергия тратится только на образование новой поверхности.

Согласно закону сохранения энергии А. Гриффитс определил, что при растяжении бесконечной пластины длиной 2 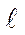трещина начнет рас-пространяться после того, как напряжение s достигнет критического уро-вня, при котором соблюдается равенство прироста работы, поглощаемой на разрушение металла, и прироста энергии упругих деформаций пласти-ны, освобождающейся при подрастании трещины (энергетическое условие для идеализированной схемы разрушения). То есть dU +dА = 0.

Если в сплошной растянутой пластине единичной толщины образо-вать трещину длиной 2 (рис.4.10), то потенциальная энергия деформации пластины уменьшится на

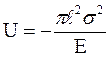(4.12)

и покажет разность потенциальной энергии деформации пластины без трещины и с трещиной в виде эллипса.

Появление новых поверхностей сопровождается затратами энергии

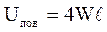,(4.13)

гдеU_пов – энергия, затрачиваемая на разрушение металла (распрост-ранение трещины).

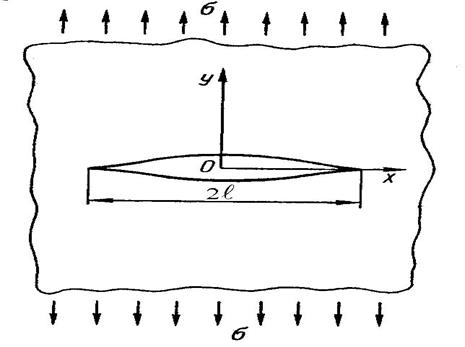
Рисунок 4.10 – Растянутая пластина с трещиной длиной 2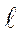

Тогда суммарное изменение энергии составит:

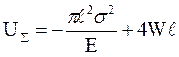.(4.14)

Если энергии освобождается больше, чем поглощается, то трещина самопроизвольно приходит в движение без увеличения напряжения. Это отвечает моменту равенства приращений высвобождаемой и затраченной энергии, то есть

.

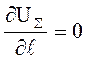Дифференцируя уравнение (4.14) по 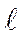, получим:

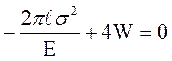(4.15)

или

.

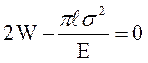По Херцбергу [20] прирост поверхностной энергии dU_пов – величи-на положительная, так как она характеризует увеличение внутренней энер-гии тела, а прирост потенциальной энергии деформации dU – величина от-рицательная, так как часть энергии выделяется телом через релаксацию напряжений в связи с появлением новых свободных от нагрузки поверхно-стей тела.

Отсюда: критическое напряжение для плоского напряженного состо-яния

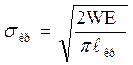; (4.16)

критическая длина трещины

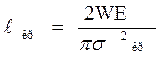; (4.17)

критическая энергия

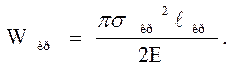(4.18)

Таким образом, достаточно зарегистрировать значение напряжения в момент начала движения трещины, чтобы вычислить по формуле характе -

ристику металла W.

Характер условия равновесия поглощаемой и высвобождаемой энер-гии определяется второй производной:

.

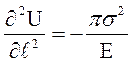Так как это выражение отрицательное, то состояние равновесия, опи-сываемое равенством (4.14) становится нестабильным и поэтому трещина постоянно растет.

Суть теоремы - максимальное разрушающее напряжение имеет место не при возникновении трещины, а после достижения ею некоторого крити- ческого размера. Существуют безопасные трещины, которые, однако, мо-гут перейти в опасные за счет хрупкости материала, снижения температу-ры, старения материала, динамического действия нагрузки.

Опыты показывают, что пластическая деформация развивается вбли- зи вершины трещины в сравнительно тонком слое, окаймляющем ее, зави-сит от многих факторов и может составлять от нескольких десятков мик-рон до десятых долей миллиметра. Э.Орван и Д.Ирвин предложили учиты- вать энергию пластического деформирования, введя в формулу вместо действительной удельной поверхностной энергии W эффективную повер-хностную энергию:

W_эф = W + W_р, (4.19)

где W_р – работа пластического деформирования при образовании единицы поверхности.

Тогда условие квазихрупкого разрушения металлов принимает вид

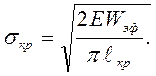(4.20)

Опыты показывают, что для сталей W_р = 10³W, поэтому в формуле (4.19) можно пренебречь значением W и предположить, что W_эф = W_р. Обозначив W_эф = W+W_Р = G, Д. Ирвин показал, что:

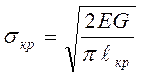-для плоского напряженного состояния. (4.21)

Для плоской деформации (если 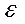_z = 0) вместо модуля упругости Е подставляется Е/(1-μ²) и формула имеет вид

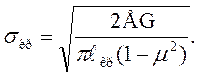(4.22)

В точке нестабильности скорость высвобождения упругой энергии G (которую также называют движущей силой распространения трещины) достигает критической величины и определяется как G_с, после чего про-исходит разрушение (распространение трещины при неизменном напря-жении).

Не следует смешивать начало движения трещины, которое связано с разрушением частиц металла по мере роста нагрузки и зоны пластических деформаций у конца трещины, с началом движения трещины по энергети-ческому условию, если напряжения в образце достигают максимально воз-можного для конкретного образца значения.

При испытании нагружением силой Р образцов крупных размеров (рис.4.11) их разрушение наступает внезапно на линейном участке диаг-раммы (рис.4.11, а) и определение К_1с и G_1с соответствует моменту мак-симальных средних напряжений σ_с. Перемещение V регистрируют напро-тив надреза с трещиной на базе АВ (рис.4.11, в, г). Если при определении К_1с и G_1с используют образцы меньших размеров, то условие плоской де-формации целиком не выдерживается и диаграмма перестает быть линей-ной (рис. 4.11, б). Поэтому применяют условную процедуру обработки ре-зультатов испытаний, проводя линию ON на 5% ниже линии упругого участка и для определения К_1с и G_1с берется напряжение σ_Q. Величины К_1с и G_1с носят название критериев Д.Ирвина.

В качестве характеристики сопротивляемости металла началу движе-ния трещины используется также и деформационный критерий – критичес-кое раскрытие трещины d_с, которое отвечает раскрытию трещины в мо-мент начала ее движения.

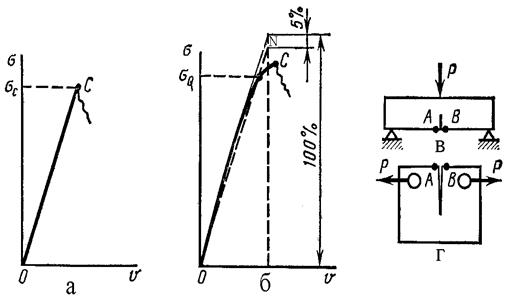
Рисунок 4.11 – Виды кривых (а, б) “нагрузка-смещение” при определении К_1с и G_1c на образцах путем их изгиба (в), или растяжения (г)

По методу Т. Каназавы 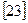(рис.4.12) образец с двумя одинаковыми надрезами (иногда с большим сечением 100 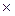100 мм) сгибают путем стати- ческого или ударного изгиба, доводят его до разрушения и определяют критерий:

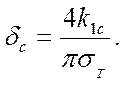(4.23)

Рисунок 4.12 – Образец с двумя надрезами для определения критерия δ_с