Математическое условие устойчивости линейных систем (2 стр. 22-23)

Как отмечалось ранее, для линейной САР общее уравнение движения может быть записано в виде:

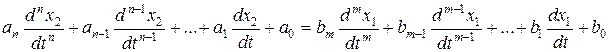(1)

Решением этого уравнения является: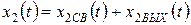

В соответствии с определением устойчивости, система будет устойчивой, если

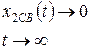(2)

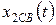является решением уравнения (1) без правой части.

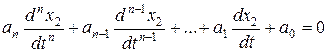(3)

В общем виде решение уравнения (3) имеет вид

(4)

где 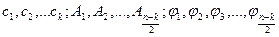- постоянные интегрирования

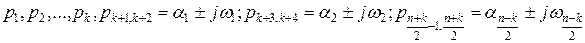- корни характеристического уравнения

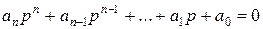
Каждому слагаемому в решении (4) с вещественным корнем соответствует процесс:

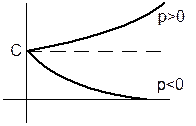
Каждому слагаемому в решении (4) с комплексным сопряженным корнем соответствует процесс:

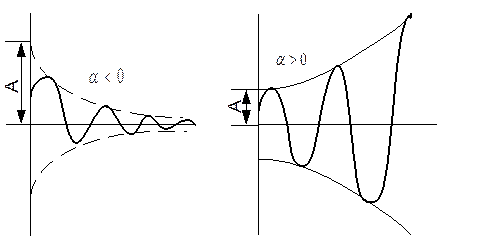
Таким образом, для устойчивости САР, описываемой линейным дифференциальным уравнением (1), необходимо и достаточно чтобы все вещественные корни характеристического уравнения и все вещественные части комплексно-сопряженных корней были отрицательны. Это условие и есть математическое условие устойчивости.

Если изобразить корни на комплексной плоскости, то математическое условие устойчивости может быть сформулировано так: для устойчивости САР, описываемой линейным дифференциальным уравнением (1) необходимо и достаточно, чтобы все корни характеристического уравнения располагались слева от мнимой оси комплексной плоскости корней. Мнимая ось является в этом случае границей устойчивости.

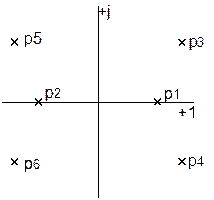
Непосредственное использование сформулированного условия возможно лишь для систем относительно невысокого порядка.

Для анализа устойчивости реальных систем используют критерии устойчивости.