Математич. описание реальных звеньев 1 порядка. (5 стр. 3-8)
Реальные динамические звенья представляют собой соединения из элементарных звеньев.
Инерционное (апериодическое) звено 1 – го порядка
Инерционным (апериодическим) звеном 1 – го порядка называется такое звено, связь между выходом и входом определяется линейным заданным уравнением 1 – го порядка вида:
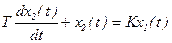, где Т – постоянная времени инерционного звена. ( 1 )
При ступенчатом изменении входного сигнала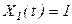 
и при пул. Начальных условиях 
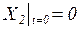решение уравнения ( 1 ) может быть представлено в виде:
| 
|
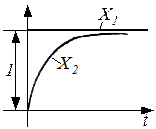
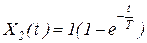
В операторной форме
|
, , 
, 
.
;
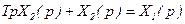
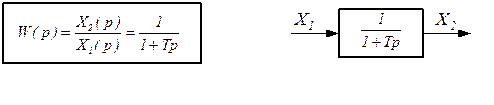
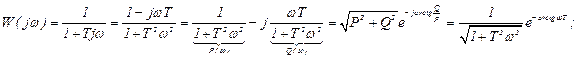
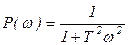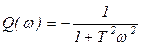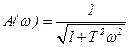
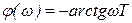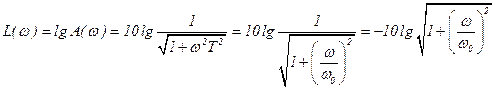при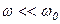 
. 
, 
;
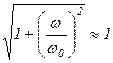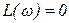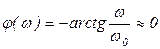при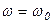 
, 
;
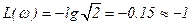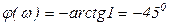при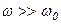 
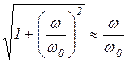
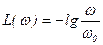- прямая с наклоном 
;
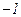при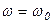 
.
|
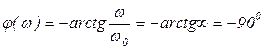Реальное дифференцирующее звено 1 – го порядка
Это звено, у которого связь между выходной и входной величиной определяется уравнением вида:
,
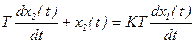где Т – постоянная времени звена
K – коэффициент усиления звена
Рассмотрим переходный процесс в таком звене при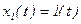 
и 
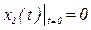
При этих условиях решение может быть записано в виде
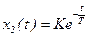, то есть при ступенчатом изменении входного сигнала выходная величина изменяется по экспоненциальной кривой.
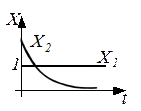
Реальные дифференцирующие звенья применяются как средство корректирования переходных процессов, например, стабилизирующий трансформатор, дифференцирующие мостовые схемы и другое.
В операционной форме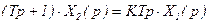 
; 
, 
,
, 
.
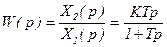
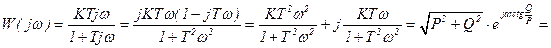
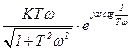
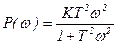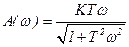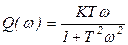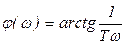при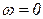 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, , 
, 
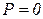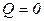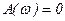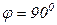
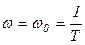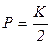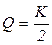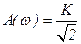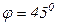
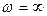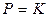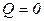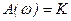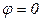
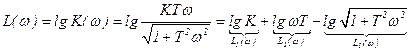
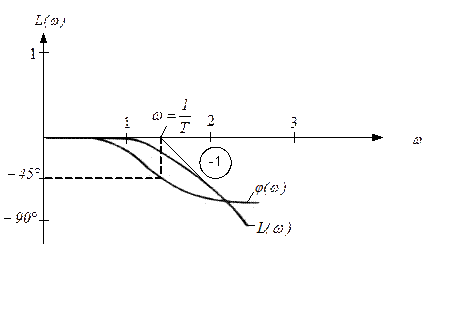
Таким образом ЛАЧХ представлена в виде 3-х составляющих:
1-я – представляет собой прямую, параллельную оси абсцисс и проходящую на уровне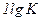 
2-я – прямая, имеющая наклон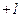 
и пересекающая ось абсцисс при .
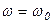3-я – представляется двумя асимптотами, сопрягающимися при 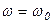причём до 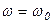асимптоты совпадают с осью абсцисс, а после имеют отрицательный наклон .
|
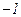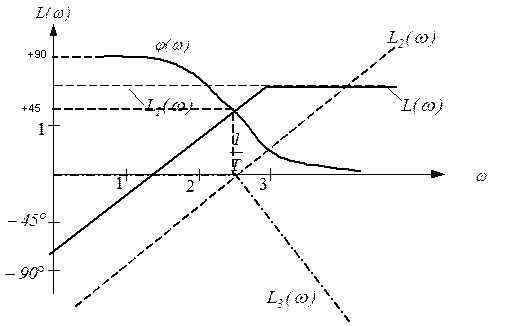
Реальное форсирующее звено 1 – го порядка
Это звено, у которого связь между выходом и входом выражается уравнением вида:
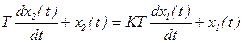
пр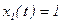и 
и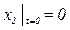 
Решение может быть представлено в виде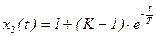 
при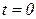 
|
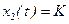
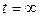
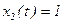
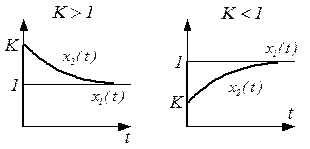
Реальное форсирующее звено наряду с реальным дифференцирующим звеном применяется как средство для корректирования, улучшения переходных процессов.
В операторной форме: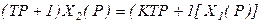 
|
,
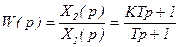
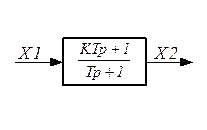
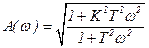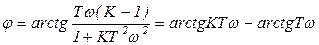
при ,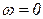 
, , 
,
, 
, 
, 
, 
, , , 
, 
, 
|
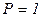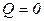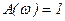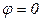
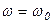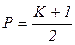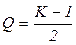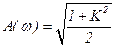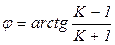
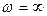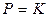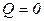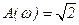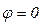
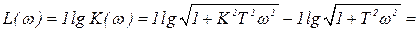
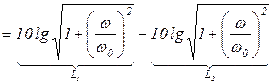
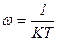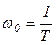
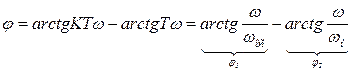
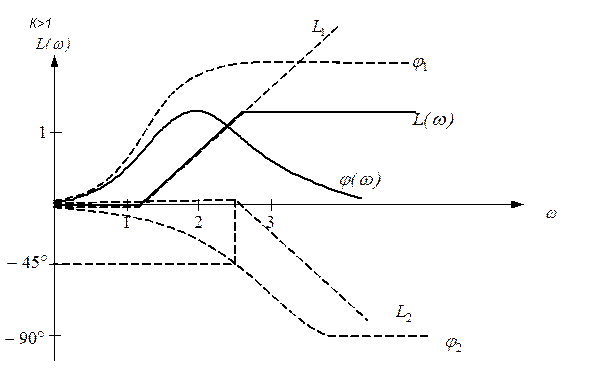
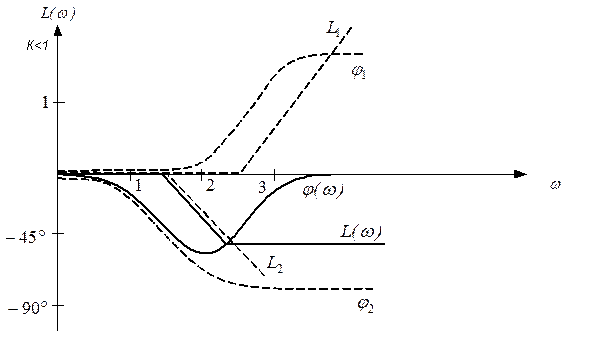
5.Передаточные ф-ции и ЧХ при различных соединениях звеньев.(3 стр. 12-14)
Дата добавления: 2015-03-20; просмотров: 736;