Частотный критерий устойчивости Михайлова
Заменим в полиноме А(р) 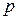 на
на 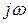 , тогда:
, тогда:
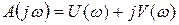 , где U – вещественная часть полинома
, где U – вещественная часть полинома 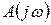 ,
,
V – мнимая часть полинома 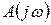 .
.
Функция 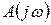 называется характеристическим вектором.
называется характеристическим вектором.
На комплексной плоскости он может быть представлен в виде вектора. При изменении 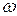 от
от 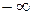 до
до 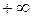 вектор
вектор 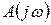 своим концом опишет в комплексной плоскости кривую, которая называется годографом Михайлова или характеристикой кривой. Поскольку функция
своим концом опишет в комплексной плоскости кривую, которая называется годографом Михайлова или характеристикой кривой. Поскольку функция 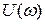 является чётной функцией
является чётной функцией 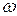 , а
, а 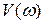 - нечётная, то годограф Михайлова симметричен относительно вещественной оси. Поэтому нет необходимости рассматривать весь годограф Михайлова, а достаточно рассмотреть лишь одну его часть, которая вычерчивает вектор
- нечётная, то годограф Михайлова симметричен относительно вещественной оси. Поэтому нет необходимости рассматривать весь годограф Михайлова, а достаточно рассмотреть лишь одну его часть, которая вычерчивает вектор 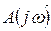 при изменении
при изменении 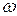 от
от 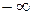 до
до 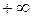 . Тогда из уравнения (*) следует, что для установившейся системы приращение аргумента вектора
. Тогда из уравнения (*) следует, что для установившейся системы приращение аргумента вектора 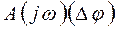 при изменении
при изменении 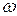 от
от 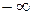 до
до 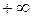 должно быть:
должно быть:
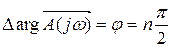
Полученное выражение и есть частотный критерий устойчивости Михайлова, в математической форме. Словами его можно выразить так:
САР устойчива тогда и только тогда, когда характеристический вектор при изменении 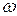 от 0 до
от 0 до 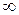 последовательно обходит число квадратов, равное порядку характ-кого уравнения, нигде не обращается в нуль
последовательно обходит число квадратов, равное порядку характ-кого уравнения, нигде не обращается в нуль
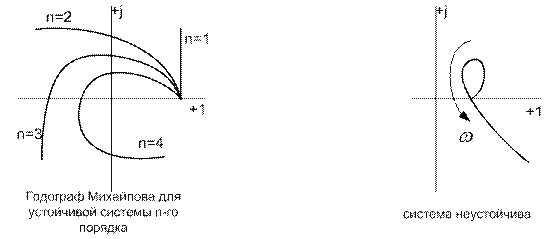
Дата добавления: 2015-03-20; просмотров: 902;
