Частотный критерий устойчивости Найквиста (2 стр. 28-29)
Критерий устойчивости Найквиста, основанный на использовании частотных характеристик, позволяет судить об устойчивости замкнутой САР по виду АФЧХ системы в разомкнутом состоянии.
Пусть дана система:
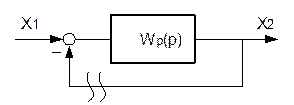
В разомкнутом состоянии передаточная функция системы:
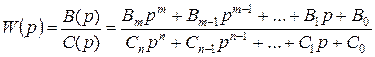
Так как 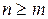 , то порядок полинома
, то порядок полинома 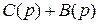 и полинома
и полинома 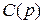 одинаков.
одинаков.
Для получения АФЧХ системы положим 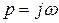
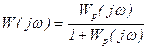 ,
,
где 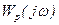 - АФЧХ замкнутой САР,
- АФЧХ замкнутой САР,
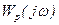 - АФЧХ разомкнутой САР.
- АФЧХ разомкнутой САР.
1.Если САР в разомкнутом состоянии устойчива, то по критерию Михайлова
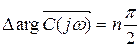
(так как порядок остается тем же), то есть в этом случае приращение аргумента вектора
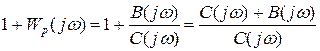
при изменении 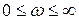 равно
равно
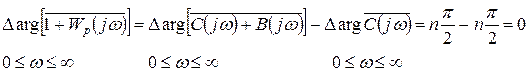 ,
,
то есть устойчивое состояние означает, что годограф вектора 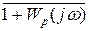 не огибает начало координат комплексной плоскости.
не огибает начало координат комплексной плоскости.
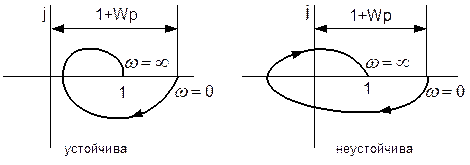
Удобно рассматривать ту же кривую, но для вектора 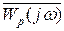 - поскольку годограф
- поскольку годограф 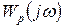 есть АФЧХ разомкнутой системы, для этого, очевидно, нужно перенести мнимую ось вправо на 1.
есть АФЧХ разомкнутой системы, для этого, очевидно, нужно перенести мнимую ось вправо на 1.
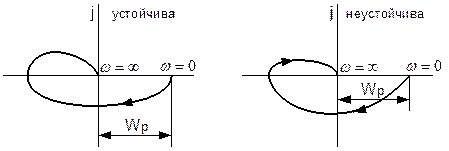
Таким образом, критерий Найквиста может быть сформулирован следующим образом:
Если система регулирования устойчива в разомкнутом состоянии, то для устойчивости замкнутой системы необходимо и достаточно, чтобы при изменении 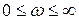 амплитудно-фазовая частотная характеристика (АФЧХ) системы в разомкнутом состоянии
амплитудно-фазовая частотная характеристика (АФЧХ) системы в разомкнутом состоянии 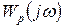 не охватывала точку с координатами
не охватывала точку с координатами 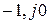 .
.
2.Рассмотрим случай, когда система в разомкнутом состоянии неустойчива, то есть характеристическое уравнение 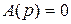 имеет q корней, лежащих в правой полуплоскости комплексной плоскости корней.
имеет q корней, лежащих в правой полуплоскости комплексной плоскости корней.
Если реальная система в разомкнутом состоянии неустойчива и имеет q корней в правой полуплоскости, то в замкнутом состоянии САУ устойчива, если АФЧХ САУ в разомкнутом состоянии 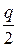 раз охватывает в положительном направлении точку с координатами
раз охватывает в положительном направлении точку с координатами 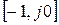
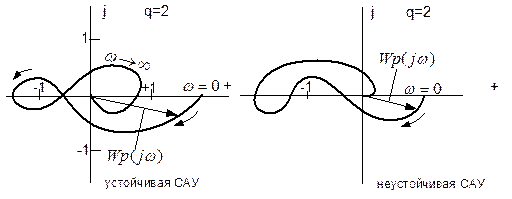
3. В случае, когда САУ в разомкнутом состоянии имеет 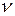 нулевых корней (
нулевых корней ( 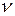 интегрирующих звеньев) анализ устойчивости замкнутой САУ можно вести аналогично случаю устойчивой САУ в разомкнутом состоянии.
интегрирующих звеньев) анализ устойчивости замкнутой САУ можно вести аналогично случаю устойчивой САУ в разомкнутом состоянии.
Если САУ в разомкнутом состоянии имеет 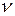 нулевых корней, то замкнутая САУ устойчива, если АФЧХ в разомкнутом состоянии дополняется окружностью бесконечно большого радиуса, начинающейся с положительной полуоси и проходящей через
нулевых корней, то замкнутая САУ устойчива, если АФЧХ в разомкнутом состоянии дополняется окружностью бесконечно большого радиуса, начинающейся с положительной полуоси и проходящей через 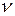 квадрантов, не огибает точку с координатами
квадрантов, не огибает точку с координатами 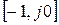 .
.
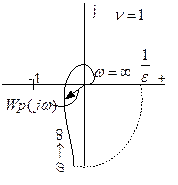
Дата добавления: 2015-03-20; просмотров: 949;
