Частотные критерии устойчивости Михайлова (2 стр. 26-27)
В основу частотных критериев исследования устойчивости САР положено следующее:
Если расположить корень рi характеристического уравнения в комплексной плоскости и рассматривать вектор 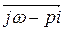 при изменении
при изменении 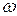 от
от 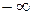 до
до 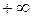 , то каждый вектор
, то каждый вектор 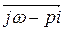 повернется на угол
повернется на угол 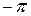 , если корень рi расположен в правой части комплексной плоскости и на угол
, если корень рi расположен в правой части комплексной плоскости и на угол 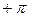 , если корень рi расположен в левой части комплексной плоскости.
, если корень рi расположен в левой части комплексной плоскости.

Таким образом, если принять, что k корней характеристического уравнения n-порядка имеют положительную вещественную составляющую, а (n-k) – отрицательную, то полином А(р)
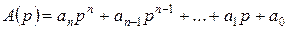 (1)
(1)
при замене 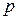 на
на 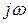 и изменении
и изменении 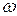 от
от 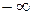 до
до 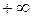 получит приращение аргумента:
получит приращение аргумента:
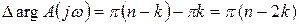 . (*)
. (*)
Для установившейся системы при изменении 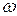 от
от 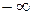 до
до 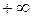
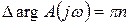 , для неустановившейся
, для неустановившейся 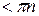 .
.
Дата добавления: 2015-03-20; просмотров: 861;
