Примеры и их решение
Пример 1. По известным напряжениям вычислить деформации в за-данной точке А.
По формуле (2.29) находим σ0, а по формуле (2.28) –  0 и подстав-ляем в формулы (2.32). Значение
0 и подстав-ляем в формулы (2.32). Значение  і определяем, используя эксперимен-тальную диаграмму зависимости σі от
і определяем, используя эксперимен-тальную диаграмму зависимости σі от  і (рис.2.13), предварительно вы-числив σі по формуле (2.19). Полученные данные подставляем в зависи-мости (2.32) и определяем
і (рис.2.13), предварительно вы-числив σі по формуле (2.19). Полученные данные подставляем в зависи-мости (2.32) и определяем  х,
х,  в ,
в ,  z, γху, γyz , γzx.
z, γху, γyz , γzx.
Пример 2. Стержень длиной 25см и диаметром 0,3 см растягивается нагрузкой 5000Н. Диаметр стержня уменьшился до 0,25 см. Определить действительные напряжения и деформации, условные напряжения и деформации, условные и действительные сужения.
Из зависимости 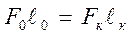 определяем конечную длину стерж-ня:
определяем конечную длину стерж-ня:
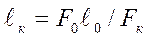 =
= 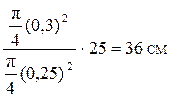 .
.
Действительные напряжения и деформации при заданной нагрузке будут соответственно равны:
σд = Р/F1 = 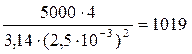 МПа,
МПа,
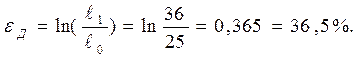
Условные напряжения и деформации при заданной нагрузке будут равны:


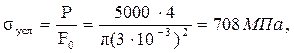
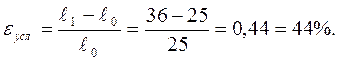
Относительное (условное) и действительное сужения при заданной нагрузке равны:
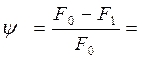
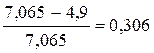 = 30,6%,
= 30,6%,

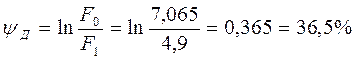 .
.
То есть, 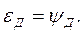
Пример 3. Образец испытывается на ползучесть и нагружен силой 6000 Н. Исходная длина круглого стержня составляла 300 мм, а началь-ный диаметр – 5 мм. После испытаний длина образца составила 350 мм. Определить действительные напряжения и деформации; условные напря-жения и деформации, относительное и действительное удлинения.
Находим диаметр стержня после испытаний:
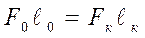 ;
;
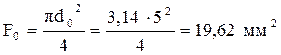 ;
;
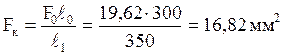 ;
;
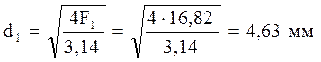 .
.
Действительные напряжения и деформации при заданной нагрузке будут соответственно равны:
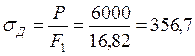 МПа,
МПа,
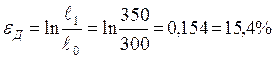 .
.
Условные напряжения и деформации при заданной нагрузке будут соответственно равны:
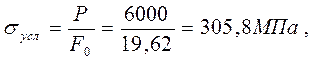
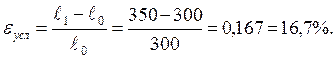
Относительное (условное) и действительное сужения равняются:
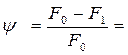
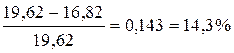 ,
,
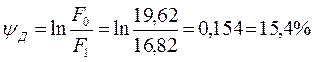 .
.
Проверка: 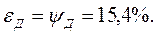
Пример 4. На гранях элемента (рис. 2.15), вырезанного из цилин-дрической стенки резервуара, действуют напряжения 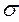 1=150 МПа,
1=150 МПа, 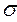 2=75МПа,
2=75МПа, 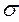 3=0. Резервуар изготовлен из малоуглеродистой стали марки Ст.3. Допускаемое напряжение на растяжение
3=0. Резервуар изготовлен из малоуглеродистой стали марки Ст.3. Допускаемое напряжение на растяжение 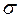 =160 МПа. Необходимо проверить прочность стенки.
=160 МПа. Необходимо проверить прочность стенки.
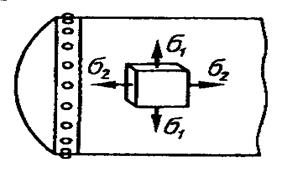
Рисунок 2.15
Так как материал находится в пластическом состоянии, то расчеты необходимо выполнять по 4 – й или 3 – й теории прочности.
Условие прочности по 4 –й теории при 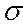 3=0 имеет вид
3=0 имеет вид
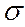 экв =
экв = 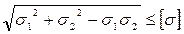 .
.
Подставляя в выражение значения 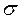 1 и
1 и 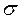 2, находим:
2, находим:
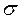 экв =
экв = 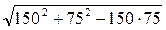 =129,9МПа < 160 МПа.
=129,9МПа < 160 МПа.
С учетом 3 - й теории прочности имеем:
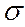 экв =
экв = 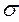 1 -
1 - 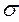 3
3 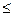
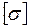 ,
,
или 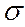 экв =150 – 0 = 150
экв =150 – 0 = 150 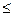 160 МПа.
160 МПа.
Таким образом, прочность стенки обеспечена.
Пример 5. По граням элемента вследствие нагрузки действуют напряжения: σ1 = 350 МПа, σ2 = 200 МПа, σ3 = 150 МПа. Принимая значе-ние модуля упругости Е=206·103 МПа и коэффициента Пуассона μ = 0,3, определить эквивалентные напряжения при одноосном, двухосном и трехосном действии напряжений и деформаций при трехосном действии напряжений.
В общем виде эквивалентные напряжения и деформации определя-ются формулами:
σі = 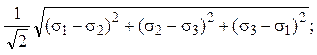
 і=
і= 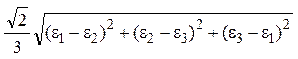 .
.
При объемном (трехосном) нагружении
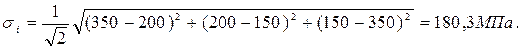
При двухосном нагружении (σ2 = 0; σ3 = σ1 = 350 МПа)
σі = 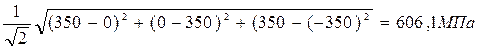 .
.
При одноосном нагружении (σ2 = 0, σ3 = 0):
σі= 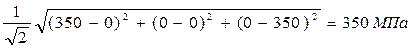 .
.
Обобщенный закон Гука для трехосного напряженного состояния имеет вид:
 1=
1= 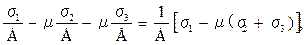
 2 =
2 = 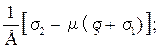
 3 =
3 = 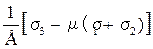 ;
;
 1 =
1 = 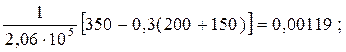
 2 =
2 = 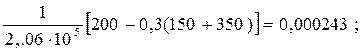
 3 =
3 = 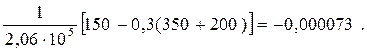
Эквивалентная деформация
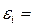
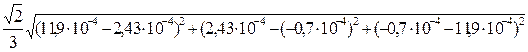 = =0,00076.
= =0,00076.
Объемная деформация
 v =
v = 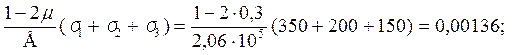
 v =
v =  1+
1+  2 +
2 +  3 =
3 = 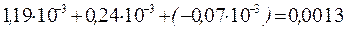 .
.
Пример 6  . Брус плотно вставлен между двумя неподвижными стенками и подлежит сжатию равномерно распределенным по горизонта-льным граням силой Р (рис. 2.16).
. Брус плотно вставлен между двумя неподвижными стенками и подлежит сжатию равномерно распределенным по горизонта-льным граням силой Р (рис. 2.16).


Рисунок 2.16
Пренебрегая трением между брусом и стенками, найти усилие давления на его стенки и изменение его размеров при Р = 10000 Н,
Е = 2 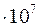 Н/см2;
Н/см2; 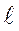 = 50 см; b = 25 см; h = 10 см.
= 50 см; b = 25 см; h = 10 см.
Напряжения давления, возникающие в продольном направлении, яв-ляются следствием действия вертикальной нагрузки, так как брус не может перемещаться в горизонтальном направлении (препятствуют недвижные стенки). Тогда имеем:
σ1 = 0; σ2 = - N / вh; σ3 = -Р/ в 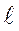 .
.
Через N обозначим давление стенок на брус. Так как в условиях при-мера размер 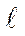 не изменяется, то
не изменяется, то  2 = 0. Из формулы
2 = 0. Из формулы
 2 =
2 = 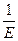 (σ2 - μσ3) = 0
(σ2 - μσ3) = 0
находим: σ2 = μσ3 = - 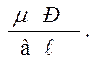
Тогда N = - вhσ2 = - вh(-μР/в)  =
= 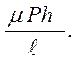
Изменение размеров бруса составит:
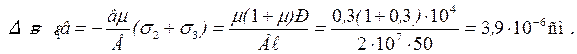
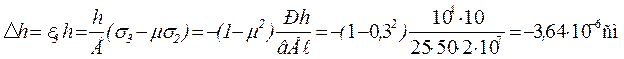
Относительное изменение объема бруса составит:
 v=
v= 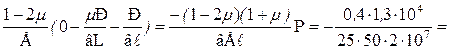
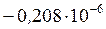 .
.
Изменение объема бруса составит:
DV =  v V =
v V =  v в h
v в h 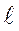 = -(1-2μ)(1+μ)
= -(1-2μ)(1+μ) 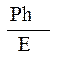 =
=
= - (1-2  0,3)(1+0,3)
0,3)(1+0,3) 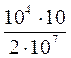 = - 0,26
= - 0,26 
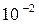 мм3.
мм3.
Дата добавления: 2015-01-10; просмотров: 1117;
