Плоское напряженное состояние, плоская деформация.

Плоское напряженное состояние (σ_z=0; 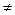0)

Плоская пластина нагружена в ее плоскости (рис.2.13, а). Толщина её δ очень мала по сравнению с размерами а и с. Если выделить элемент с размерами dх, dy и δ в любой точке пластины, то на его гранях возникнут напряжения σ_х, σ_y, τ_xy и τ_yx (рис.2.13, б).

На боковых гранях этого элемента напряжения отсутствуют: σ_z = 0; τ_zx =0; τ_zy = 0, и мы имеем плоское напряженное состояние тела, то есть две параллельных грани бесконечно малого элемента, выделенного в любой точке тела, свободны от напряжений. Напряжения σ_х, σ_y, τ_xy и τ_yx равномерно распределены по толщине пластины.

Рисунок 2.13 – Схема определения плоского напряженного состояния

При плоском напряженном состоянии в каждой точке изменяется толщина пластины. Деформация в направлении оси Z по закону Гука равна:

.

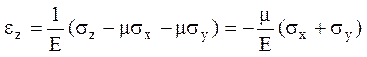Толщина пластины в каждой точке вследствие поперечной деформации изменяется на величину 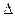δ = _zδ = - 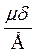(σ_x + σ_y).

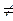Плоская деформация( _z = 0; σ_z 0)

Имеем очень длинное цилиндрическое тело, равномерно нагружен-ное по всей длине в (рис.2.14, а). Мысленно рассечем это тело на отде-льные слои толщиной δ=1. Если бы эти слои испытывали плоское напря-женное состояние, то в каждой точке пластины толщина изменялась бы на величину Δδ. Но в результате противодействия соседних слоёв это невоз-можно, поэтому каждый слой деформируется в условиях (рис.2.14, б), где он как бы зажат между двумя абсолютно твердыми поверхностями, прину-дительно обеспечивающими условия неизменяемости толщины слоя

Δδ = 0. При этом перемещение во всех точках тела происходит только в параллельных плоскостях XY (см.рис.2.14, б). Так как перемещения W, U, V относительно оси Z отсутствуют, то имеем:

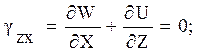
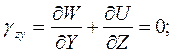
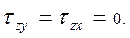
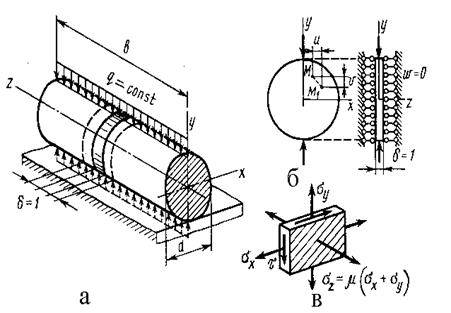
Рисунок 2.14 – Схема определения плоской деформации

Это и есть плоская деформация. По закону Гука имеем:

_z = (σ_z - μσ_x - μσ_y) / E = 0 .

В местах, где пластина должна была утолщаться, появятся сжимаю-щие напряжения σ_z , а в местах возможного утонения – растягивающие напряжения σ_z(рис.2.14,в) В обоих случаях

σ_z = μ(σ_x + σ_y). (2.44)