Замечания к разделу

Плавное спадание гауссовой функции наводит на представление о клубке как об объекте относительно плотном в центре и более рыхлым на периферии. Это неверно. Балабаев смоделировал на ЭВМ тепловое движение идеальной цепи из 626 звеньев и показал, что цепочка совершенно не заполняет объема клубка. Распределение Гаусса возникает только после усреднения по огромному числу разных конформаций, откуда видно, сколь значительна роль флуктуаций плотности в полимерном клубке.

Представление об идеальной цепочке плодотворно, но оно недостаточно для понимания большинства явлений в полимерных системах: необходим учет взаимодействия звеньев разных макромолекул, а также сблизившихся не соседних звеньев одной полимерной цепи, т.е. учет объемных взаимодействий. Возникает вопрос, как проявляется то факт, что полимерная цепь не бестелесная, каждое звено имеет объем, и внутренность этого объема недоступна для других звеньев. Эту проблему исключенного объема можно сформулировать также как задачу о случайных блужданиях частицы (звена), избегающей пересекать свой след.

Размер идеального Гауссова клубка R~lN^1/2. Клубок занимает объем ~R³~l³N^3/2. Но полимерная цепь не заполняет этот объем. Если собственный объем звена V, то общий объем макромолекулы N•V. При N>>1 l³N^3/2>>V•N, т.е. доля объема, занятого звеньями внутри клубка, очень мала:

φ ~ ~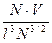

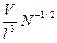
Это в какой-то мере оправдывает представление об идеальном клубке: раз плотность мала, то столкновения звеньев редки. Считая клубок облаком независимых частиц-звеньев, распределенных в объеме l³N^3/2, можно оценить число столкновений. Число двойных столкновений оценивают так: есть N частиц, и на каждую из них с вероятностью φ налетает партнер, значит, число двойных столкновений ~Nφ, число тройных Nφ², четверных Nφ³ и т.д.

Число р-кратных столкновений:

N_p~ Nφ^p-1~N^(3-p)/2 .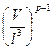

Видно, что число многократных столкновений редко: N_p<<1 при p>3. Даже число тройных столкновений ~1 на всю длинную цепь. Число двойных - ~N^1/2, т.е. хотя и мало по сравнению с N (т.е. каждое звено сталкивается редко), но велико по сравнению с 1.

С другой стороны, клубок очень податлив, модуль упругости его мал ~1/N. Поэтому можно ожидать, что парные столкновения звеньев приведут к существенному изменению фактических размеров клубка.

Первая теория набухания полимерного клубка в хорошем растворителе была предложена Флори: равновесное набухание клубка определяется компенсацией расталкивающего влияния исключенного объема и стягивающей энтропийной упругости. Как и ожидалось, несмотря на чрезвычайную рыхлость клубка и малую вероятность столкновений, эффект исключенного объема очень велик: при N 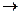¥ параметр набухания неограниченно возрастает.