Осмотическое давление полимерного раствора

Макромолекулы создают избыток давления со своей стороны от мелкопористой перегородки (давление растворителя с обеих сторон одинаково). Этот избыток и есть осмотическое давление.

В разбавленном растворе (с<<c^*) не перекрывающихся клубков (с – концентрация полимера в растворе, с^* - концентрация полимера в клубке) осмотическое давление – это избыток давления за счет давления клубков на перегородку. Поскольку число клубков в единице объема пропорционально с/N, осмотическое давление: 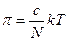, N>>1 (число звеньев).

Когда концентрация полимерного раствора достигает с^*, клубки начинают перепутываться и в полуразбавленном растворе при c>>c^*, отталкивание звеньев дает больший вклад в давление, чем поступательное броуновское движение целых клубков.

По теории Флори для осмотического давления получили бы p~kT•Bc² (В – второй вириальный коэффициент, B=a³, a – размер звена).

Согласно скейлинговым рассуждениям клубки имеют единственный характерный макроскопический размер – размер R клубка как целого. Тем самым есть лишь одна характерная концентрация N/R³~c^* и поэтому осмотическое давление:

,

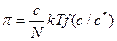где f – функция, которую и требуется определить.

В полуразбавленном растворе, т.е. при с/с^*>>1 было установлено: f(с/с^*)~(с/с^*)^5/4, т.е. .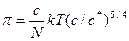

Иными словами, был получен существенно отличающийся от теории Флори результат. Причина расхождения заключается в том, что в теории Флори флуктуации концентрации звеньев никак не учитываются. Разбавленные и неразбавленные растворы полимерных клубков сильно флуктуируют, и пренебрежение флуктуациями для этих систем приводит к значительным ошибкам.

Скейлинговые рассуждения есть, по сути дела, простой способ получить результаты точной флуктуационной теории. Эксперименты полностью подтвердили скейлинговую формулу p»с^9/4 (а не p~kTBc²~kTa³c², а – длина звена).

С ростом концентрации различие этих результатов уменьшается. Это указывает на то, что по мере концентрирования роль флуктуаций уменьшается, в концентрированном растворе они вообще несущественны.