Средние молекулярные массы
Закономерности, по которым данные физические свойства зависят от молекулярной массы, также определяют способ усреднения, который должен быть применен в каждом случае. Таким образом, при рассмотрении различных физических свойств мы неизбежно должны применить различные средние молекулярные массы. Особенно важны среднечисловая и средневесовая, встречаются также средневискозиметрическая и «Z-средняя» молекулярные массы.
Среднечисловая 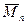 получается путем суммирования количества молекул каждого сорта, умноженных на их молекулярную массу, и деления на общее число молекул. Для любой смеси молекул:
получается путем суммирования количества молекул каждого сорта, умноженных на их молекулярную массу, и деления на общее число молекул. Для любой смеси молекул:
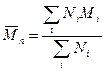 , где Ni – число молекул сорта i, имеющихся в смеси, Mi – их молекулярная масса.
, где Ni – число молекул сорта i, имеющихся в смеси, Mi – их молекулярная масса.
Вместо числа молекул Ni мы можем использовать число молей ni, число молекул или молей в единице объема или мольную долю. Удобно пользоваться мольными долями 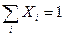 и
и 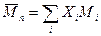 .
.
Если смесь представляет собой чистый полимерный образец, в котором молекулы различаются только по степени полимеризации, то х для различных сортов молекул будет меняться от 1 до ¥ и их молекулярные массы будут равны Мх=хМо так, что:
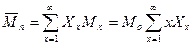
Среднечисловая степень полимеризации определяется также:
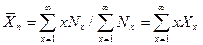 ,
,
где Nx – число х-мерных молекул или их количество в единице объема.
Средневесовая молекулярная масса. 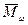 получают путем сложения числа граммов gi полимера, молекулы которого имеют молекулярную массу Mi, умноженного на эту молекулярную массу, и деления на общую массу полимера в граммах. Можно использовать также концентрацию г/мл или весовую долю Wi :
получают путем сложения числа граммов gi полимера, молекулы которого имеют молекулярную массу Mi, умноженного на эту молекулярную массу, и деления на общую массу полимера в граммах. Можно использовать также концентрацию г/мл или весовую долю Wi :
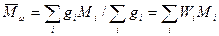
И если полимер состоит из одинаковых звеньев, то:
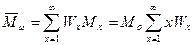 ,
, 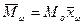
Средневесовая степень полимеризации:
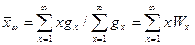 ,
,
где Wx – весовая доля.
Общее определение для 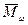 можно записать другим способом.
можно записать другим способом.
Так как масса i-го сорта молекул gi, очевидно, равна NiMi/NA, то:
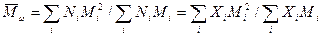
Используя выражения для Wx и Хх, полученные нами ранее для:
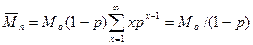 ,
,

и 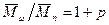 . При р®1
. При р®1 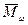 @2
@2 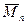 .
.
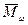 и
и 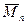 встречаются очень часто. Реже более высокие формы средних величин:
встречаются очень часто. Реже более высокие формы средних величин:
Z-средний - 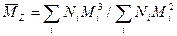
Z+1-средний - 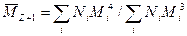
Суммирование по всем возможностям i. Если образец полностью гомогенен, то во всех случаях
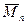 =
= 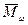 =
= 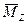 =
= 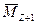
Разность вязкости полимерного раствора и соответствующего растворителя часто может быть пропорциональна произведению весовой концентрации и Мa, где a - константа (0,5-2,0=a). Для гетерогенного образца получают средневискозиметрический молекулярный вес 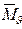 .
.
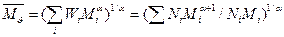
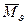 =
= 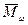 , если a=1,0. При a<1,0
, если a=1,0. При a<1,0 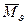 является промежуточным между
является промежуточным между 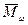 и
и 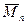 .
.
Дата добавления: 2015-02-07; просмотров: 3946;
