Взаимосвязь массы и энергии.
Энергия 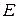 тела (без учета потенциальной энергии во внешнем силовом поле) связана с его массой
тела (без учета потенциальной энергии во внешнем силовом поле) связана с его массой 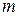
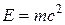 , (77)
, (77)
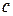 - скорость света в вакууме.
- скорость света в вакууме.
Энергия покоя тела
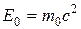 ,
,
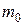 - масса покоящегося тела.
- масса покоящегося тела.
Кинетическая энергия релятивистской частицы
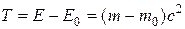 .
.
8. Связь между энергией 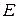 и импульсом
и импульсом 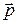 частицы.
частицы.
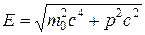 . (78)
. (78)
Образец теста по разделу «Механика»
1. Материальная точка движется по окружности радиусом 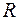 = 5 м так, что пройденный ею путь меняется со временем как
= 5 м так, что пройденный ею путь меняется со временем как 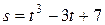 м. Определить величину ускорения
м. Определить величину ускорения 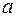 точки в момент
точки в момент 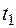 = 2 с. В произвольной точке траектории показать направления тангенциального, нормального и полного ускорения материальной точки.
= 2 с. В произвольной точке траектории показать направления тангенциального, нормального и полного ускорения материальной точки.
(Ответ: ≈ 20 м/с2 )
2. Диск вращается равнозамедленно в направлении, показанном на рисунке. Определить номер линии, по которой направлен вектор углового ускорения 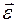 .
.
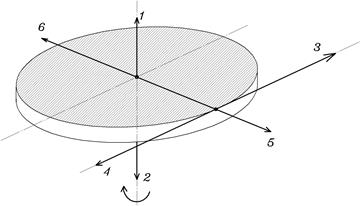 (Ответ: 1)
(Ответ: 1)
3. В каком случае скорость 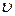 тела можно вычислить по формуле
тела можно вычислить по формуле 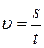 ? Указать номер правильного ответа.
? Указать номер правильного ответа.
1: 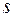 =6
=6 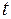 м 2:
м 2: 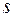 =6
=6 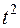 м 3:
м 3: 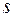 =(6
=(6 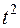 +
+ 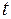 ) м 4:
) м 4: 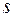 =(6
=(6 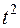 +1) м
+1) м
(Ответ: 1)
4. Тело массой 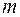 = 2 кг падает вертикально вниз с ускорением
= 2 кг падает вертикально вниз с ускорением 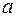 =9 м/с2 . Определить среднюю силу сопротивления воздуха.
=9 м/с2 . Определить среднюю силу сопротивления воздуха.
(Ответ: 2 Н)
5. Четыре шарика массами 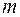 , 2
, 2 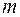 , 3
, 3 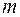 , 4
, 4 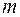 закреплены на невесомом стержне на одинаковом расстоянии
закреплены на невесомом стержне на одинаковом расстоянии 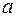 = 0,1 м друг от друга. На каком расстоянии от крайнего левого шарика находится центр масс системы?
= 0,1 м друг от друга. На каком расстоянии от крайнего левого шарика находится центр масс системы?
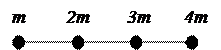
(Ответ: 20 см)
6. Четыре шарика одинаковой массы 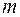 = 50 г закреплены невесомыми стержнями в вершинах квадрата со стороной
= 50 г закреплены невесомыми стержнями в вершинах квадрата со стороной 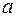 = 10 см. Определить момент инерции
= 10 см. Определить момент инерции 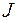 системы относительно оси
системы относительно оси 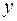 . Шарики рассматривать как материальные точки.
. Шарики рассматривать как материальные точки.

(Ответ: 0,001 кг· м2)
7. Чтобы закатить барабан радиуса 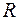 = 1 м на ступеньку высотой
= 1 м на ступеньку высотой 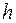 = 50 см, к нему прикладывают горизонтальную силу
= 50 см, к нему прикладывают горизонтальную силу 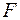 = 2 Н. Определить величину момента
= 2 Н. Определить величину момента 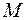 этой силы относительно точки О.
этой силы относительно точки О.
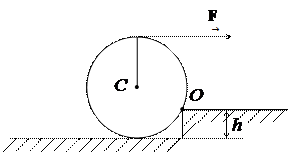 |
(Ответ: 3 Н· м)
8. С какой угловой скоростью 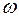 должен вращаться диск радиуса
должен вращаться диск радиуса 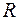 = 0,8 м и массой
= 0,8 м и массой 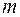 = 0,5 кг, чтобы его кинетическая энергия
= 0,5 кг, чтобы его кинетическая энергия 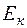 составляла 2 Дж?
составляла 2 Дж?
(Ответ: 5 рад/c)
9. Стержень длиной 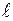 = 1 м ставят вертикально на конец
= 1 м ставят вертикально на конец 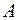 и отпускают. Стержень падает без проскальзывания, вращаясь вокруг точки
и отпускают. Стержень падает без проскальзывания, вращаясь вокруг точки 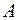 . Определить угловое ускорение
. Определить угловое ускорение 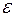 стержня в момент, когда он составляет угол
стержня в момент, когда он составляет угол 
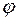 = 60° с плоскостью.
= 60° с плоскостью. 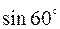
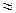 0,9;
0,9; 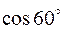 =0,5.
=0,5.
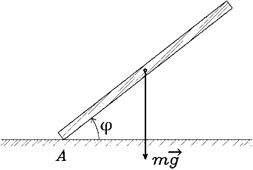 |
(Ответ: 7,5 рад/с2)
 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Тема «Кинематика»
Пример 1.Частица движется по окружности радиусом 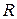 = 50 см так, что зависимость ее пути
= 50 см так, что зависимость ее пути 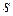 от времени
от времени 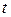 имеет вид
имеет вид 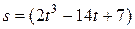 м. Определить скорость
м. Определить скорость 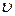 и ускорение
и ускорение 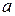 частицы в момент
частицы в момент 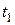 =2 с. Найти угол
=2 с. Найти угол 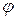 между скоростью и ускорением частицы в заданный момент времени.
между скоростью и ускорением частицы в заданный момент времени.
Дано: 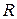 =0,5 м,
=0,5 м, 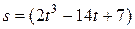 м ,
м , 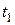 =2 с. Найти:
=2 с. Найти: 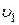 ,
, 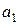 ,
, 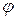 .
.
Решение. Скорость представляет собой производную от пути по времени
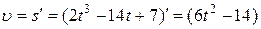 м/c .
м/c .
В момент 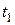 =2 с,
=2 с,
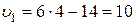 м/c .
м/c .
Тангенциальное ускорение
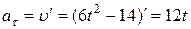 м/c2,
м/c2, 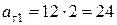 м/c2 .
м/c2 .
Нормальное ускорение
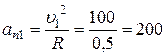 м/c2.
м/c2.
Полное ускорение 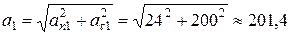 м/c2 .
м/c2 .
Скорость  и
и  направлены по касательной к окружности,
направлены по касательной к окружности, 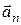 - к ее центру (рис.10).
- к ее центру (рис.10).
Рисунок 10 –Направления скорости и ускорения.
 ;
;  .
.
Ответ: 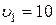 м/c ,
м/c , 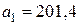 м/c2 ,
м/c2 , 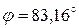 .
.
Пример 2. Цилиндр радиусом 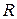 катится без скольжения со скоростью
катится без скольжения со скоростью 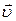 (рис.11). Определить скорости точек А и В, а также радиусы кривизны их траекторий.
(рис.11). Определить скорости точек А и В, а также радиусы кривизны их траекторий.
Дано: 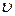 ,
, 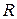 . Найти:
. Найти: 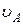 ,
, 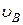 ,
, 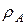 ,
, 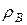 .
.
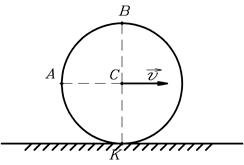
Рис. 11.
Решение.
1). Качение цилиндра можно представить как сумму двух движений: поступательного с постоянной скоростью 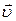 (рис.12,
(рис.12, 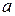 ) и вращательного вокруг центра масс
) и вращательного вокруг центра масс 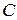 (рис.12,
(рис.12, 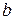 ).
).
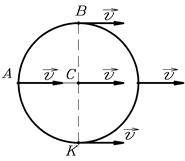
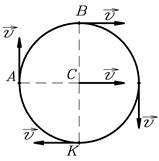
Рис.12, 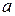 . Рис.12,
. Рис.12, 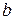 .
.
Т.к. скорость точки К касания цилиндра с землей равна нулю, то значит, при вращении точки обода цилиндра движутся также со скоростью 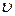 . В результате сложения скоростей при поступательном и вращательном движениях находим скорости точек
. В результате сложения скоростей при поступательном и вращательном движениях находим скорости точек 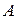 и
и 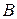
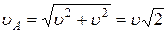 ;
; 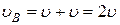 .
.
Направления векторов  и
и  показаны на рисунке 13.
показаны на рисунке 13.
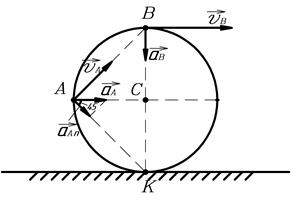
Рис.13.
2). Ускорение точек 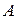 и
и 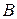 обусловлено вращением цилиндра,
обусловлено вращением цилиндра,
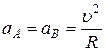 .
.
Векторы 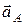 и
и 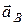 направлены к центру
направлены к центру 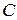 цилиндра. Нормальное ускорение точки
цилиндра. Нормальное ускорение точки 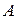 перпендикулярно скорости
перпендикулярно скорости 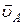 (рис.13),
(рис.13),
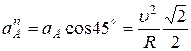 .
.
Нормальное ускорение точки 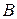 равно ее полному ускорению
равно ее полному ускорению
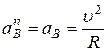 .
.
Т.к. радиус кривизны траектории 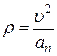 , то
, то
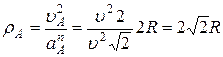 ,
,
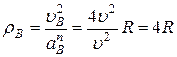 .
.
Ответ: 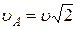 ,
, 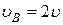 .
. 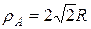 ,
, 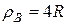 .
.
Тема «Законы Ньютона»
Пример 3. Тело скользит по наклонной плоскости, составляющей угол 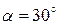 с горизонтом. Пройденный телом путь
с горизонтом. Пройденный телом путь 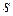 меняется со временем
меняется со временем 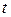 по уравнению
по уравнению 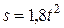 м. Определить коэффициент трения
м. Определить коэффициент трения 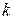 тела о плоскость.
тела о плоскость.
Дано: 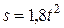 м,
м, 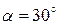 . Найти:
. Найти:  ..
..
Решение. Скорость тела равна
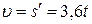 м/c.
м/c.
Ускорение тела
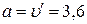 м/c2.
м/c2.
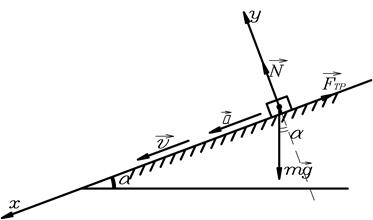
Рис.14.
При движении на тело действуют сила тяжести 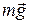 , сила трения
, сила трения 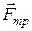 , сила реакции опоры
, сила реакции опоры  (рис.14).
(рис.14).
Запишем 2-ой закон Ньютона 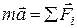 в проекциях на оси x и y :
в проекциях на оси x и y :
(x) 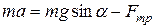 , (1)
, (1)
(y) 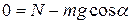 . (2)
. (2)
Из (1): 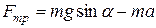 ,
,
из (2): 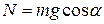 .
.
Т.к. 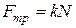 , то коэффициент трения
, то коэффициент трения
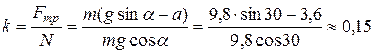 .
.
Ответ: 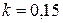 .
.
Пример 4. Сфера радиусом 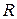 =1 м равномерно вращается вокруг вертикального диаметра с частотой 36 мин-1. Внутри сферы находится шарик массой
=1 м равномерно вращается вокруг вертикального диаметра с частотой 36 мин-1. Внутри сферы находится шарик массой 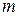 =50 г. Найти, на какой высоте, отсчитываемой от нижней точки сферы, шарик займет положение равновесия относительно сферы. Определить силу давления шарика на сферу в этом положении.
=50 г. Найти, на какой высоте, отсчитываемой от нижней точки сферы, шарик займет положение равновесия относительно сферы. Определить силу давления шарика на сферу в этом положении.
Дано: 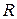 =1 м,
=1 м, 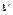 =36 мин-1=0,6 с-1,
=36 мин-1=0,6 с-1, 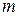 =0,05 кг. Найти:
=0,05 кг. Найти: 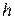 ,
, 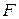 .
.
Решение: На шарик действуют сила тяжести 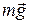 и реакция опоры
и реакция опоры  (рис.15).
(рис.15).
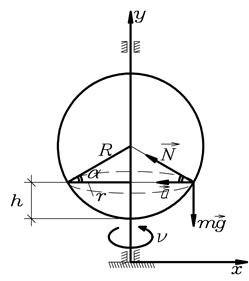
Рис.15.
Т.к. вращение равномерное, то тангенциальное ускорение шарика
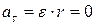 .
.
Полное ускорение шарика равно нормальному,
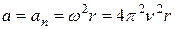 ,
,
и направлено к центру его траектории. Т.к. радиус траектории 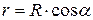 , то
, то
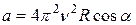 . (1)
. (1)
Запишем 2-ой закон Ньютона для шарика в проекции на оси x и y
(x) 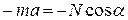 , (2)
, (2)
(y) 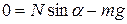 . (3)
. (3)
Отсюда 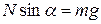 и
и 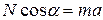 . Поделим два последних уравнения одно на другое,
. Поделим два последних уравнения одно на другое,
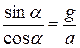 .
.
Подставим из (1) выражение для ускорения
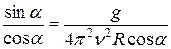 .
.
Отсюда 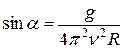 .
.
Т.к. 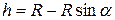 , то
, то
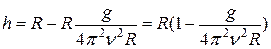 .
.
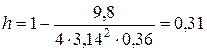 м =
м = 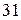 см.
см.
Из (3) найдем, что 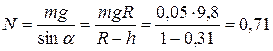 Н.
Н.
Сила давления шарика на сферу численно равна силе реакции опоры, 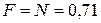 Н.
Н.
Ответ: 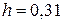 м ;
м ; 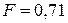 Н.
Н.
Тема «Импульс тела. Центр масс»
Пример 5. Шарик массой 50 г, движущийся со скоростью 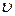 =2 м/с под углом
=2 м/с под углом 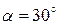 к стенке, абсолютно упруго соударяется с ней. Продолжительность удара
к стенке, абсолютно упруго соударяется с ней. Продолжительность удара 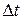 =0,01 с. Определить среднюю силу, действующую на стенку во время удара.
=0,01 с. Определить среднюю силу, действующую на стенку во время удара.
Дано: 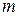 =0,05 кг,
=0,05 кг, 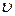 =2 м/c,
=2 м/c, 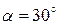 ,
, 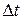 =0,01 c. Найти:
=0,01 c. Найти: 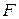 .
.
Решение. Изменение количества движения (импульса) шарика равно сумме импульсов действующих на него сил:
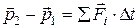 . (1)
. (1)
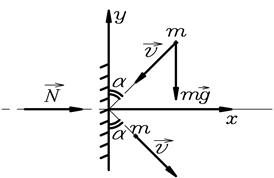
Рис.16.
На шарик действуют сила тяжести 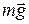 и, во время удара, сила реакции стенки
и, во время удара, сила реакции стенки  (рис.16).
(рис.16).
Спроецируем уравнение (1) на ось x:
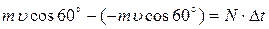 .
.
Отсюда
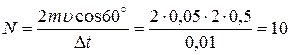 Н.
Н.
Т.к. сила, действующая на стенку, численно равна силе реакции опоры, то
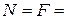 10 Н.
10 Н.
Ответ: 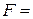 10 Н.
10 Н.
Пример 6. Четыре точечные массы 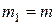 ,
, 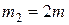 ,
, 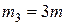 и
и 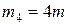 находятся в вершинах квадрата со стороной
находятся в вершинах квадрата со стороной 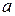 (рис.17). Определить положение центра масс данной системы.
(рис.17). Определить положение центра масс данной системы.
Дано: 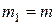 ,
, 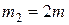 ,
, 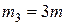 ,
, 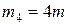 ,
, 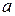 . Найти:
. Найти: 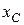 -?
-? 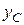 -?
-?
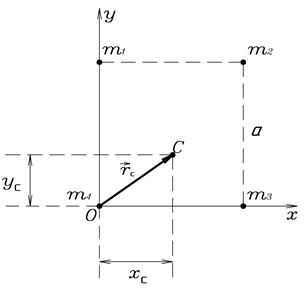
Рис.17.
Решение. Расположим начало координатных осей x и y в точке  . Тогда координаты центра масс
. Тогда координаты центра масс 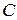 равны
равны
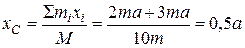 ,
,
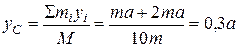 .
.
Величина радиус-вектора центра масс
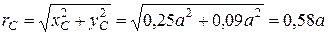 .
.
Ответ: 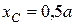 ,
, 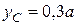 .
.
Тема «Динамика вращательного движения»
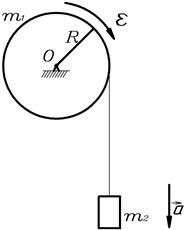
Пример 7. На барабан массой 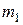 =3 кг намотан шнур, к концу которого привязан груз массой
=3 кг намотан шнур, к концу которого привязан груз массой 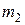 =2 кг (рис.18). Найти ускорение
=2 кг (рис.18). Найти ускорение 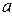 груза и силу натяжения
груза и силу натяжения 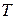 шнура, считая барабан однородным диском. Трением пренебречь.
шнура, считая барабан однородным диском. Трением пренебречь.
 Дано:
Дано: 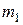 =3 кг,
=3 кг, 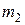 =2 кг,
=2 кг,
барабан – диск. Найти: 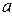 ,
, 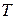 .
.
Решение. На груз действуют
сила тяжести 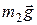 и сила
и сила
натяжения шнура 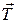 (рис.19) .
(рис.19) .
Т.к. груз совершает
поступательное движение,
запишем для него 2-ой закон Ньютона Рис.18
в проекции на ось y, направленную
вертикально вниз, Рис.18.
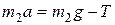 . (1)
. (1)
На барабан действуют сила натяжения 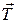 , сила тяжести
, сила тяжести 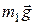 и реакция опоры
и реакция опоры  (рис.20).
(рис.20).
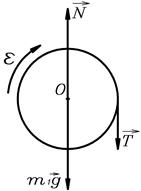
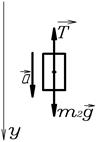
Рис.19. Рис.20.
Т.к. барабан вращается, воспользуемся основным законом динамики вращательного движения 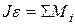 и запишем его относительно оси вращения, проходящей через точку
и запишем его относительно оси вращения, проходящей через точку 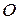 :
:
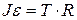 , (2)
, (2)
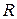 - радиус барабана. Моменты сил
- радиус барабана. Моменты сил  и
и 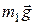 относительно точки
относительно точки 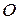 равны нулю.
равны нулю.
Т. к. барабан – однородный диск, его момент инерции
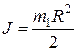 .
.
Угловое ускорение барабана 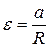 . Подставив
. Подставив 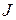 и
и 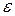 в уравнение (2), получаем
в уравнение (2), получаем
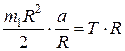 . (3)
. (3)
Отсюда 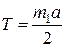 . (4)
. (4)
Подставим 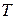 в (1):
в (1):
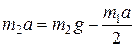 .
.
Тогда 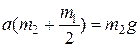 .
.
Отсюда ускорение
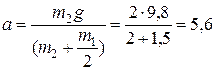 м/с2.
м/с2.
Сила натяжения шнура из уравнения (4):
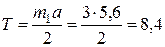 Н.
Н.
Ответ:  м/c2 ,
м/c2 , 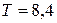 Н.
Н.
Пример 8. Лестница массой 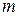 =16 кг приставлена к вертикальной стене под углом 20° к ее поверхности. На лестнице на расстоянии
=16 кг приставлена к вертикальной стене под углом 20° к ее поверхности. На лестнице на расстоянии 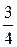 ее длины , от нижнего конца, стоит человек массой
ее длины , от нижнего конца, стоит человек массой 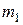 =75 кг. Каким должен быть коэффициент трения между основанием лестницы и поверхностью пола, чтобы лестница не соскользнула? Трением между лестницей и стенкой пренебречь.
=75 кг. Каким должен быть коэффициент трения между основанием лестницы и поверхностью пола, чтобы лестница не соскользнула? Трением между лестницей и стенкой пренебречь.
Дано: 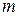 =16 кг,
=16 кг, 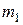 =75 кг,
=75 кг, 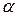 =20°,
=20°, 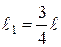 . Найти:
. Найти: 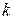 .
.
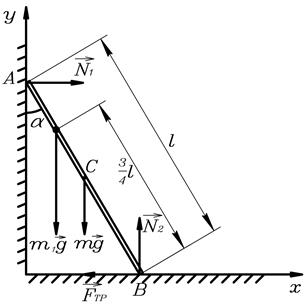
Рис.21.
Решение. Обозначим 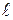 - длина лестницы. На лестницу с человеком действуют сила тяжести лестницы
- длина лестницы. На лестницу с человеком действуют сила тяжести лестницы 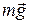 , человека
, человека 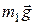 , сила трения
, сила трения 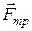 и реакции опор
и реакции опор 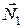 и
и 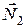 (рис.21).
(рис.21).
Т.к. система находится в равновесии, то сумма действующих на нее сил и моментов сил должна быть равна нулю.
Запишем условие равенства нулю суммы сил в проекции на ось y:
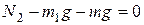 .
.
Отсюда 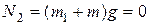 .
.
Запишем условие равенства нулю моментов сил, относительно точки 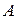 :
:
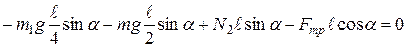 .
.
Сокращая на 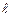 и учитывая, что
и учитывая, что 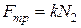 , получаем
, получаем
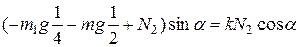 .
.
Отсюда 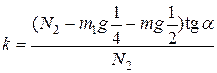 =
= 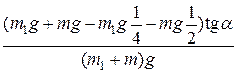 =
=
= 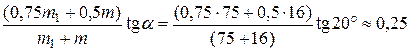
Ответ: 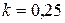 .
.
Тема «Работа. Механическая энергия»
Пример 9. Тонкий стержень длиной 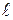 =0,8 м может свободно вращаться вокруг вертикальной оси, проходящей его верхний конец. Стержень отклонили на угол
=0,8 м может свободно вращаться вокруг вертикальной оси, проходящей его верхний конец. Стержень отклонили на угол 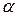 =60 ° и отпустили (рис.22). Определить угловую скорость
=60 ° и отпустили (рис.22). Определить угловую скорость  стержня, линейную скорость его нижнего конца и скорость центра масс
стержня, линейную скорость его нижнего конца и скорость центра масс  в момент прохождения стержнем положения равновесия.
в момент прохождения стержнем положения равновесия.
Рис.22.
Дано: 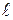 =0,8 м,
=0,8 м, 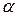 =60 °. Найти:
=60 °. Найти: 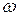 ,
, 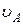 ,
, 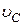 .
.
Решение.
Изменение кинетической энергии стержня равно работе сил, приложенных к нему:
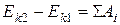 (1)
(1)
(теорема о кинетической энергии).
В начальный момент стержень неподвижен, 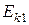 =0.
=0.
В момент прохождения положения равновесия 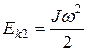 ,
,
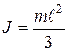 - момент инерции однородного стержня относительно оси вращения, проходящей через точку подвеса
- момент инерции однородного стержня относительно оси вращения, проходящей через точку подвеса  . Тогда
. Тогда
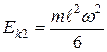 . (2)
. (2)
На стержень действуют сила тяжести 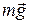 и реакция опоры
и реакция опоры  . Сила
. Сила  не совершает работы, т.к. точка ее приложения неподвижна. Работа силы тяжести
не совершает работы, т.к. точка ее приложения неподвижна. Работа силы тяжести
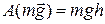 .
.
Т.к. 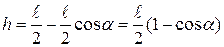 , то
, то
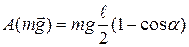 . (3)
. (3)
Подставляя в (1) уравнения (2) и (3), получаем
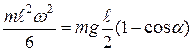 .
.
Отсюда 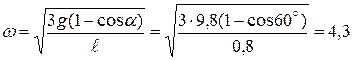
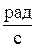 .
.
Скорость точки  ,
, 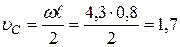 м/с.
м/с.
Скорость точки  ,
, 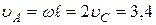 м/с.
м/с.
Ответ: 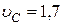 м/с,
м/с, 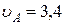 м/с.
м/с.
Пример 10. Шар, движущийся со скоростью 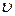 =4 м/с, закатывается на наклонную плоскость, составляющую угол
=4 м/с, закатывается на наклонную плоскость, составляющую угол 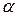 = 30° с горизонтом (рис.23). Какое расстояние
= 30° с горизонтом (рис.23). Какое расстояние 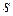 пройдет шар по наклонной плоскости за счет его кинетической энергии? Трением пренебречь.
пройдет шар по наклонной плоскости за счет его кинетической энергии? Трением пренебречь.
Дано: 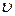 =4 м/с,
=4 м/с, 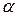 = 30° . Найти:
= 30° . Найти: 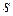 .
.
Решение. Применим теорему о кинетической энергии:
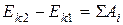 . (1)
. (1)
В конце движения шар останавливается, поэтому 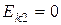 .
.
Начальная кинетическая энергия шара
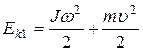 , (2)
, (2)
т.к. движение шара складывается из поступательного и вращательного. В формуле (2) 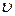 - скорость центра масс
- скорость центра масс 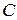 шара (рис.23).
шара (рис.23).
Момент инерции шара 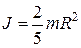 , его угловая скорость
, его угловая скорость 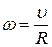 .
.
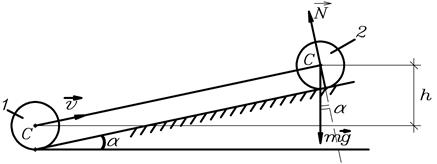
Рис.23.
Тогда 
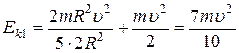 (3)
(3)
Сила реакции опоры  работы не совершает. Работа силы тяжести
работы не совершает. Работа силы тяжести
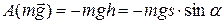 . (4)
. (4)
Подставляя выражения для 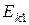 и
и 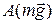 в (1), получаем
в (1), получаем
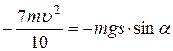 .
.
Отсюда 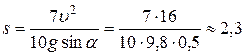 м.
м.
Ответ: 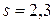 м.
м.
Тема «Уравнения гидродинамики»
Пример 11. Вода из трубы диаметром 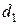 =5 см, расположенная на глубине 1 м, поступает в здание под давлением 3 атм со скоростью 0,5 м/с. На верхнем этаже на высоте 10 м труба сужается до диаметра
=5 см, расположенная на глубине 1 м, поступает в здание под давлением 3 атм со скоростью 0,5 м/с. На верхнем этаже на высоте 10 м труба сужается до диаметра 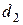 =2,5 см. Вычислить скорость течения и давление в трубе на верхнем этаже (вязкостью воды пренебречь).
=2,5 см. Вычислить скорость течения и давление в трубе на верхнем этаже (вязкостью воды пренебречь).
1 атм=101,3∙103 Па.
Дано: 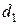 =5 см=5∙10-2 м,
=5 см=5∙10-2 м, 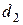 =2,5 см=2,5∙10-2 м,
=2,5 см=2,5∙10-2 м, 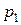 =3 атм=303,9∙103 Па,
=3 атм=303,9∙103 Па, 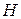 =1 м,
=1 м, 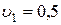 м/с,
м/с, 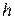 =10 м. Найти:
=10 м. Найти: 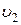 ,
, 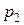 .
.
Решение. Из уравнения неразрывности вычислим скорость движения воды в узком сечении трубы
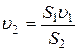 .
.
Т.к. площади сечений 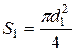 и
и 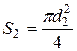 , то
, то
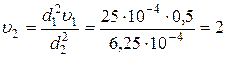 м/с .
м/с .
Уравнение Бернулли
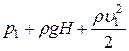 =
= 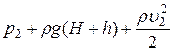 .
.
Отсюда
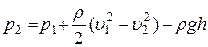 .
.
Подставим числовые данные, учитывая, что плотность воды 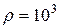 кг/м3 ,
кг/м3 , 
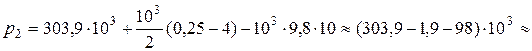
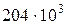 Па.
Па.
Ответ: 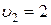 м/с ,
м/с , 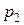 =204∙103 Па.
=204∙103 Па.
Пример 12. Для измерения скорости протекания газа используют трубку Вентури (трубку с сужением, в которую врезан жидкостный манометр, рис.24).
Определить скорость движения газа 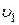 в широкой части трубки, если известны плотность
в широкой части трубки, если известны плотность 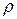 газа и плотность
газа и плотность 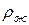 жидкости, площади
жидкости, площади 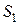 и
и 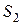 сечений трубки, разность уровней
сечений трубки, разность уровней 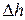 жидкости в манометре.
жидкости в манометре.
Дано: 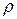 ,
, 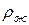 ,
, 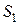 ,
, 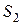 ,
, 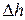 . Найти:
. Найти: 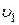 .
.
Решение. Т.к. трубка тока газа расположена горизонтально, то уравнение Бернулли для нее имеет вид
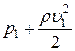 =
= 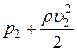 , (1)
, (1)
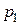 и
и 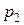 - статическое давление газа в широком сечении 1 и в узком сечении 2.
- статическое давление газа в широком сечении 1 и в узком сечении 2.
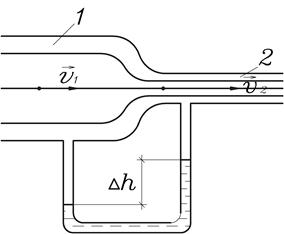
Рис.24.
Из (1):
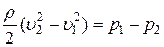 . (2)
. (2)
Разность статических давлений 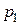 и
и 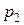 уравновешивается гидростатическим давлением столбика жидкости высотой
уравновешивается гидростатическим давлением столбика жидкости высотой 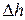
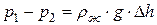 . (3)
. (3)
Из (2):
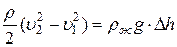 . (4)
. (4)
Скорости 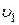 и
и 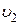 связаны уравнением неразрывности
связаны уравнением неразрывности
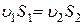 .
.
Отсюда 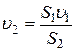 . Подставим
. Подставим 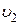 в (4):
в (4):
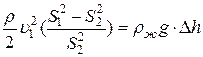 .
.
Получаем 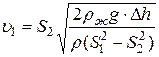 .
.
Ответ: 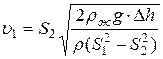 .
.
Дата добавления: 2015-03-20; просмотров: 2147;
