Упругость полимерной цепи с исключенным объемом

Модуль упругости идеальной цепочки, растягиваемой за концы силой f: 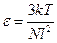и ~ ( ).

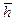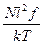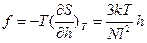Упругость обусловлена тепловым движением, т.е. флуктуациями конформаций, а флуктуации в клубке имеют макроскопический характер. Отсюда следует, что упругое поведение клубка должно зависеть от его общего размера R~l•N^g (для идеальной цепи g=1/2, для цепи с исключенным объемом g=3/5), но не от каких-либо микроскопических параметров звеньев. Поскольку для реальных цепей с исключенным объемом g=3/5, видно, что h~N в степени больше единицы: h~N^r, (r>1)

Этот результат имеет простой физический смысл: в реальной цепи связи воспринимают не только внешнюю нагрузку, как в идеальной цепи, но еще и расталкивающее действие межзвенных контактов. Для реальной цепи g=3/5 получается нелинейная зависимость растяжения от силы h~f^2/3, т.е. мы видим, что полимерный клубок с исключенным объемом ведет себя под действием внешней нагрузки совсем не так, как идеальная цепь.

Анализируя эти рассуждения, можно отметить, что главным явилось предположение о том, что из всех характеристик клубка упругие свойства зависят лишь от его общего размера lN^g, т.е. что этот размер является единственным характерным масштабом клубка. В этом предположении заключена так называемая гипотеза масштабной инвариантности, или скейлинга (scale – масштаб). Теории, основанные на этой гипотезе, называются скейлинговыми. Самым важным в скейлинговых теориях является учет флуктуаций плотности звеньев.